MATCH EXPONENTIAL FUNCTIONS AND GRAPHS

Match the equation with the graph (the asymptotes are shown on the graph)

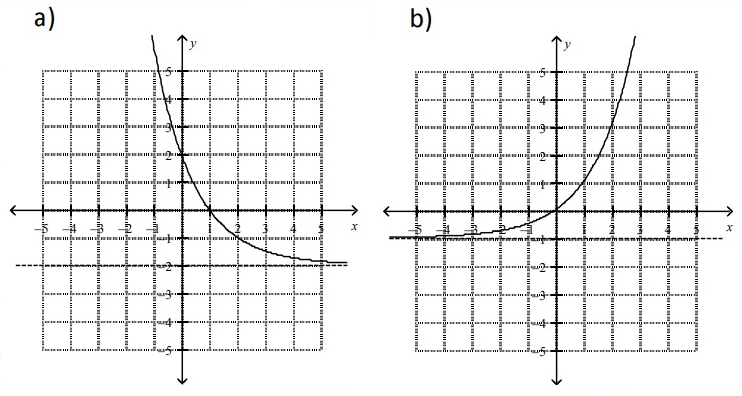
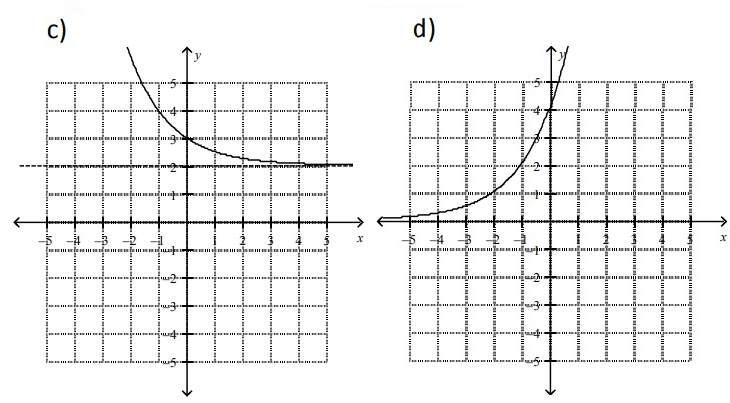
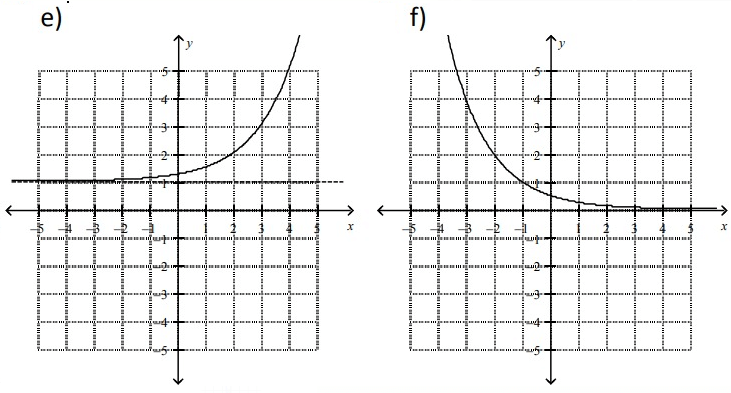
Problem 1 :

f(x) = 4(0.5)^x - 2

Problem 2 :

f(x) = 4(2)^x

Problem 3 :

f(x) = (0.5)^x+1

Problem 4 :

f(x) = (0.5)^x + 2

Problem 5 :

f(x) = 2^x-2 + 1

Problem 6 :

f(x) = 2^x - 1

Problem 1 :

f(x) = 4(0.5)^x - 2

Solution:

Finding Horizontal asymptote:

Comparing the equation with y = a b^{(x - h)} + k

f(x) = 4(0.5)^x - 2

Here b = 0.5 it lies between 0 to 1, it is decay function.

Equation of horizontal asymptote will be in the form y = k

Here k = -2

Then the horizontal asymptote will be y = -2.

Finding x and y intercept:

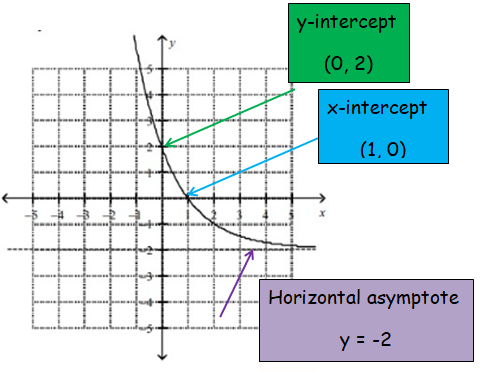
So, graph (a) is correct.

Problem 2 :

f(x) = 4(2)^x

Solution:

Finding Horizontal asymptote:

Comparing the equation with y = a b^{(x - h)} + k

f(x) = 4(2)^x 

Here b = 2 it is greater than 1, it is growth function.

Equation of horizontal asymptote will be in the form y = k

Here y = 0

Then the horizontal asymptote will be y = 0

Finding x and y intercept:

Put x = 0

y = 4(2)⁰

y = 4

So, graph (d) is correct.

Problem 3 :

f(x) = (0.5)^x+1

Solution:

Finding Horizontal asymptote:

Comparing the equation with y = a b^{(x - h)} + k

f(x) = (0.5)^x+1

Here b = 0.5 it lies between 0 and 1, it is decay function.

Equation of horizontal asymptote will be in the form y = k

Here y = 0

Then the horizontal asymptote will be y = 0

Finding y intercept:

Put x = 0

y = (0.5)⁰⁺¹

y = 0.5

So, the y-intercept is (0, 0.5).

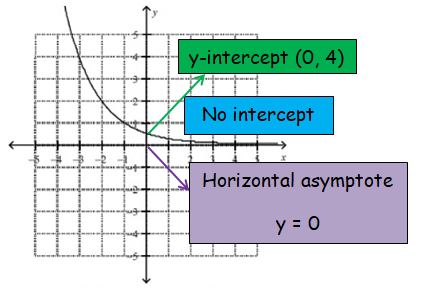
So, graph (f) is correct.

Problem 4 :

f(x) = (0.5)^x + 2

Solution:

Finding Horizontal asymptote:

Comparing the equation with y = a b^{(x - h)} + k

f(x) = (0.5)^x + 2

Here b = 0.5 it lies between 0 and 1, it is decay function.

Equation of horizontal asymptote will be in the form y = k

Here y = 2

Then the horizontal asymptote will be y = 2

Finding y intercept:

Put x = 0

y = (0.5)⁰ + 2

y = 1 + 2

y = 3

So, the y-intercept is (0, 3).

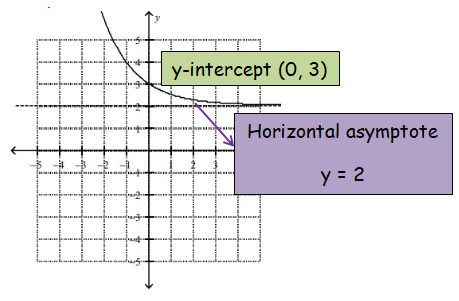
So, graph (c) is correct.

Problem 5 :

f(x) = 2^x-2 + 1

Solution:

Finding Horizontal asymptote:

Comparing the equation with y = a b^{(x - h)} + k

f(x) = 2^x-2 + 1

Here b = 2 is greater than 1, it is growth function.

Equation of horizontal asymptote will be in the form y = k

Here y = 1

Then the horizontal asymptote will be y = 1

Finding y intercept:

Put x = 0

y = 2^0-2 + 1

y = 1/4 + 1

y = 5/4

So, the y-intercept is (0, 1.25).

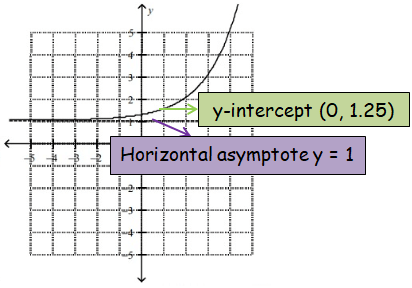
So, graph (e) is correct.

Problem 6 :

f(x) = 2^x - 1

Solution:

Finding Horizontal asymptote:

Comparing the equation with y = a b^{(x - h)} + k

f(x) = 2^x - 1

Here b = 2 is greater than 1, it is growth function.

Equation of horizontal asymptote will be in the form y = k

Here y = -1

Then the horizontal asymptote will be y = -1

Finding y intercept:

Put x = 0

y = 2⁰ - 1

y = 1 - 1

y = 0

So, the y-intercept is (0, 0).

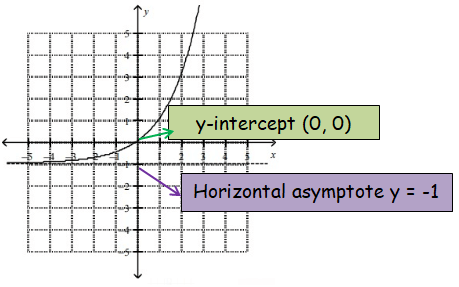
So, graph (b) is correct.