LINES AND SLOPES PRACTICE PROBLEMS IN SAT

Problem 1 :

In the xy plane, the lines

y = mx - 7 are 2x + 3y = 6

are parallel. What is the value of m ?

Solution :

Slope of the line y = mx - 7 :

By comparing the given equation with slope intercept form

y = mx + b

m₁ = m

Slope of the line 2x + 3y = 6 :

3y = -2x + 6

Dividing by 3 on both sides.

y = (-2/3) x + (6/3)

y = (-2/3) x + 2

m₂ = -2/3

Since the given lines are parallel,

m₁ = m₂

m = -2/3

Problem 2 :

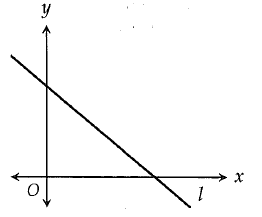
The graph of the line l is shown in the xy plane above. The equation of line n (not shown) is y = mx + b, where m and b are constants. If line l is perpendicular to the line n, which of the following must be true ?

(a)  m < 0     (b) m > 0       (c)  b < 0     (d) b > 0

Solution :

The given graph shows line (l) is a falling line and it will have negative slope.

If we draw the line which is perpendicular to the given line, it must be a raising line. 

Raising line will have positive slope. So, m > 0

Problem 3 :

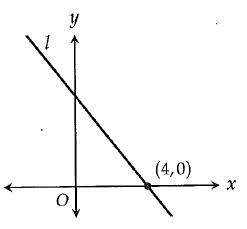
In the xy plane above, line l has slope -5/4. What is the area of the triangle bounded by the line l, the x-axis and the y-axis ?

(a)  5    (b)  8     (c)  10     (d)  16

Solution :

Since it is a falling line, it will have negative slope.

Rise = 5 and run = 4

Area of the triangle = (1/2) x base x height

Base = 4 and height = 5

= (1/2) x 5 x 4

= 10

Problem 4 :

In the xy plane, the line with the equation 3x + 4y = 6 is perpendicular to the line with the equation y = mx + b, where m and b are constants. What is the value of m ?

(a)  4/3    (b)  -4/3     (c)  3/4     (d)  -3/4

Solution :

Slope of the line  3x + 4y = 6 :

4y = -3x + 6

y = (-3/4) x + (6/4)

y = (-3/4) x + (3/2)

Slope of the line = -3/4

Slope of the perpendicular line = -1/(-3/4)

= - 4/3

Problem 5 :

If m and b are real numbers and m > 0 and b > 0 then the line whose equation is y = mx + b cannot contain which of the following points ?

(a)  (0, 1)     (b)  (1, 1)      (C)  (-1, 1)      (d) (0, -1)

Solution :

Since m > 0, it should be a raising line and it has positive y-intercept.

Then, it should be in the first and second quadrants, in the given set of options (d) contains the point from fourth quadrant.

So, (0, -1) is not one of the points on the line.

Problem 6 :

In which of the following figures is the slope of the line shown closest to -1/2 ?

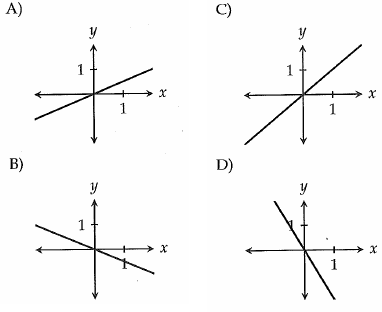
Solution :

By observing the options, B and D are falling line, they will have negative slopes.

In -1/2, Rise = 1 and run = 2 units. So, option D is correct.

Problem 7 :

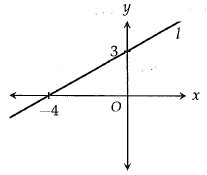
The graph of the line l is shown in the xy plane above. The y-intercept of the line l is 3 and the x-intercept is -4. If the line m is perpendicular to line l, what is the slope of the line m ?

(a)  -4/3     (b)  -3/4      (C)  -1/2      (d) 3/4

Solution :

Slope of the given line is raising line, so, it will have positive slope.

Rise = 3 and run = 4

Slope of the line = 3/4

Slope of the line which is perpendicular to the line = -4/3

Problem 8 :

In the xy-plane, line l passes through (0, 0) and is perpendicular to the line 3x + y = c, where c is a constant. If two lines intersect at the point (k, k - 4), what is the value of k ?

(a)  4     (b)  6      (C)  8      (d) 10

Solution :

The line l passes through the point (0, 0) and the point of intersection of lines l and 3x + y = c is (k, k - 4).

Slope of the contains the points (0, 0) and (k, k - 4) is 

m₁ = (k - 4 - 0)/(k - 0)

m₁ = (k - 4)/k

Slope of the line 3x + y = c

y = -3x + c

m₂ = -3

Since these lines are perpendicular to each other, the product of their slopes will be equal to -1.

m1 x m2 = -1

[(k - 4)/k] (-3) = -1

-3(k - 4) = -k

3k - 12 = k

3k - k = 12

2k = 12

k = 6