LINEAR PROGRAMMING WORD PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Paul sells chocolate chip cookies and peanut butter cookies
- Baking a batch of chocolate chip cookies takes 2.4 cups of flour and 2 eggs.
- Baking a batch of peanut butter chip cookies takes 1.6 cups of flour and 1 egg.
- Paul makes 12.8 cups of flour and 10 eggs.
- He makes $4 profit per batch of chocolate chip cookies.
- He makes $2 profit per batch of peanut butter chip cookies.
How many batches of peanut butter cookies should Paul to maximize his profit.
Solution :
Let x and y be the number of batches of chocolate chip cookies and peanut butter cookies respectively.
Maximum cups of flour to be used = 12.8 cups.
2.4x + 1.6y ≤ 12.8 ----(1)
Maximum number of eggs used = 10
2x + y ≤ 10 ----(2)
Profit function :
P = 4x + 2y
Finding x and y -intercepts for (1), we get
2.4x + 1.6y ≤ 12.8
|
x-intercept, put y = 0 2.4x = 12.8 x = 12.8/2.4 x = 5.33 (5.33, 0) |
y-intercept, put x = 0 1.6y = 12.8 y = 12.8/1.6 y = 8 (0, 8) |
Finding x and y -intercepts for (2), we get
2x + y ≤ 10
|
x-intercept, put y = 0 2x = 10 x = 5 (5, 0) |
y-intercept, put x = 0 y = 10 (0, 10) |
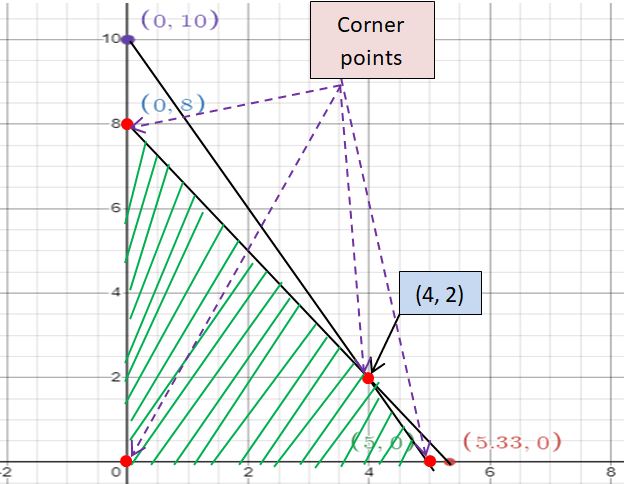
Corner points :
Let A (0, 0), B (5, 0), C (4, 2) and D (0, 8)
4x + 2y
Applying A(0, 0) :
Profit = 4(0) + 2(0)
= 0
Applying B(5, 0) :
Profit = 4(5) + 2(0)
= 20 + 0
= 20
Applying C(4, 2) :
Profit = 4(4) + 2(2)
= 16 + 4
= 20
Applying D(0, 8) :
Profit = 4(0) + 2(8)
= 16
So, the maximum profit is 20.
Problem 3 :
Projection indicate the expected demand of atleast 100 scientific and 80 graphing calculator each day.
Because of limitation of production capacity, no more than 200 scientific and 170 graphing calculator can be made daily.
To satisfy a shipping contract sold result in a $2 loss, but each graphing calculator produces $5 profit, how many of each type should made daily to maximize net profits ?
Solution :
Let x be the number of scientific calculators produced and y be the number of graphing calculator produced.
x > 100 and x ≤ 200
y > 80 and y ≤ 170
x + y ≥ 200
Profit function :
P = -2x + 5y
Problem 2 :
A company produces packs pencils and pens.
- The company produces at least 100 packs of pens each day, but no more than 240.
- The company produces at least 70 packs of pencils each day, but no more than 170.
- A total of less than 300 packs of pens and pencils are produced each day.
- Each pack of pens make a profit of $1.25
- Each pack of pencils make a profit of $0.75
what is the maximum profit the company can make each day ?
a) 338.75 b) 344.25 c) 352.50 d) 427.50
Solution :
Let x be the number of packs pencils and y be the number of packs of pens.
x > 100 and x ≤ 240
y > 70 and y ≤ 170
x + y < 300
Profit function :
1.25x + 0.75y
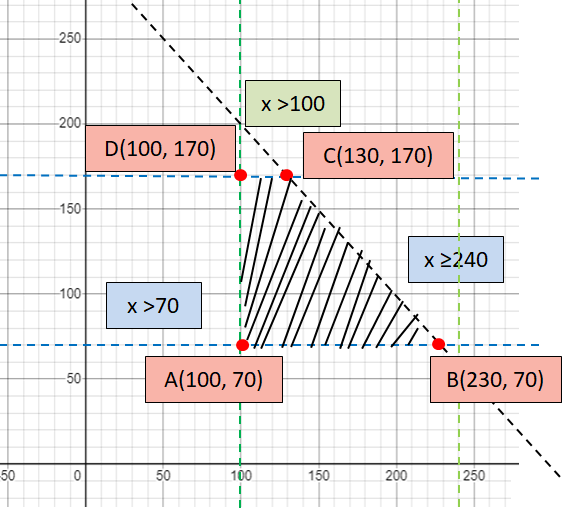
Corner points :
A (100, 70), B (230, 70), C (130, 170) and D (100, 170)
x + y < 300
Applying A(100, 70) :
Profit = 1.25(100) + 0.75(70)
= 125 + 52.5
= 177.5
Applying B(230, 70) :
Profit = 1.25(230) + 0.75(70)
= 287.5 + 52.5
= 340
Applying C(130, 170) :
Profit = 1.25(130) + 0.75(170)
= 162.5 + 127.5
= 290
Applying D(100, 170) :
Profit = 1.25(100) + 0.75(170)
= 125 + 127.5
= 252.5
So, the maximum profit is 340.
Problem 3 :
Projection indicate the expected demand of atleast 100 scientific and 80 graphing calculator each day.
Because of limitation of production capacity, no more than 200 scientific and 170 graphing calculator can be made daily.
To satisfy a shipping contract sold result in a $2 loss, but each graphing calculator produces $5 profit, how many of each type should made daily to maximize net profits ?
Solution :
Let x be the number of scientific calculators produced and y be the number of graphing calculator produced.
x > 100 and x ≤ 200
y > 80 and y ≤ 170
x + y ≥ 200
Profit function :
P = -2x + 5y
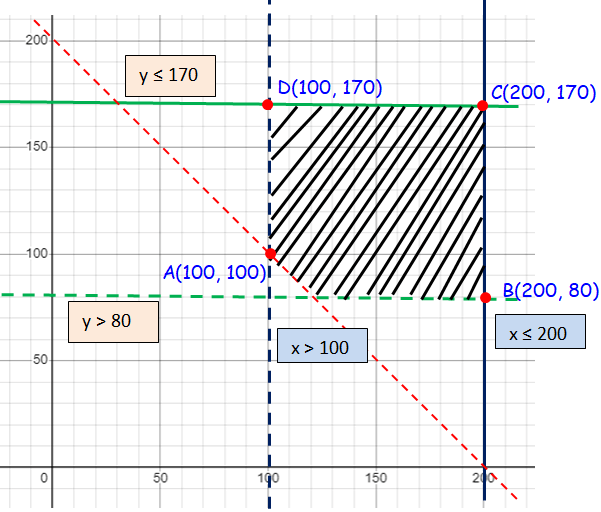
Corner points :
A (100, 100), B (200, 80), C (200, 170) and D (100, 170)
P = -2x + 5y
Applying A(100, 100) :
Profit = -2(100) + 5(100)
= 300
Applying B(200, 80) :
Profit = -2(200) + 5(80)
= -400 + 400
= 0
Applying C(200, 170) :
Profit = -2(200) + 5(170)
= -400 + 850
= 450
Applying D(100, 170) :
Profit = -2(100) + 5(170)
= -200 + 850
= 650
So, the maximum profit is $650.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling