LINEAR EQUATIONS PRACTICE FOR EOG FOR GRADE 8

Problem 1 :

A school purchases boxes of candy bars.

• Each box contains 50 candy bars.
• Each box costs $30

How much does the school have to charge for each candy bar to make a profit of $10 per box.

a)  $0.40      b) $0.50      c)  $0.80       d)  $1.25

Solution :

Let x be the cost of each candy bars in the box.

Profit can be found by subtracting selling price and cost price.

Cost price = $30, selling price = 50x

Profit = Selling price - cost price

10 = 50x - 30

50x = 10 + 30

50x = 40

x = 40/50

x = 0.80

So, cost of each candy should be $0.80 to make a profit of $10.

Problem 2 :

Cell phone company Y charges a $10 start up fee plus $0.10 per minute x. Cell phone company Z charges $0.20 per minute x with no start up fee, Which function represents the difference in cost between Company Y and Company Z

a)  f(x) = 0.10x - 10         b)  f(x) = 0.10x + 10

c)  f(x) = 10x - 0.10         d)  f(x) = 10x - 0.10

Solution :

Number of minutes = x

Company X charges :

Start up fee + cost per minute

= 10 + 0.10x -----(1)

Company Y charges :

No start up fee + cost per minute

= 0.20x -----(2)

Difference between X and Y :

(1) - (2)

f(x) = 10 + 0.10x - 0.20x

f(x) = 10 - 0.10x

So, option a is correct.

Problem 3 :

Mr. Jones determined that the equation

y = 98 - (16/5)x

could be used to predict his students’ unit test scores, based on the number of days, x, a student was absent during the unit. What is the meaning of the y-intercept of the function?

A) A student who was not absent during the unit should score about 98.

B)  A student who was not absent during the unit should score about 94.5.

C)  A student’s test score should increase by about 3.2 points for each day the student is absent.

D) A student’s test score should decrease by about 3.2 points for each day the student is absent.

Solution :

y = 98 - (16/5)x

y = -(16/5)x + 98 

Comparing the equation with y = mx + b

m = -16/5 and y-intercept = 98

So, option A is correct.

Problem 4 :

What is the value of x in the equation shown below?

0.25x + 7 = 4(x – 2)

Solution :

0.25x + 7 = 4(x – 2)

0.25x + 7 = 4x – 8

7 + 8 = 4x - 0.25x

15 = 3.75x

x = 15/3.75

x = 4

So, the value of x is 4.

Problem 5 :

What value of x satisfies the equation below? 

Solution :

Problem 6 :

The value in dollars, y, of a car x years after it was purchased can be modeled by the function

y = 14,000 – 875x

What is the meaning of the y-intercept of the linear model?

A) The initial value of the car is $14,000.

B) The average value of the car is $14,000.

C) The car’s value decreases by $875 each year after it was purchased.

D) The car’s value decreases by $16 each year after it was purchased.

Solution :

y = 14,000 – 875x

Comparing the given equation with y = mx + b

m = -875 and y-intercept = 14000

y-intercept is initial value and at the rate of 875 the value is  decreasing. So, option A is correct.

Problem 7 :

A car rental company charges $34 per day for a rented car and $0.50 for every mile driven. A second car rental company charges $20 per day and $0.75 for every mile driven. What is the number of miles at which both companies charge the same amount for a one-day rental?

A) 56 miles      B) 54 miles      C) 36 miles      D) 24 miles

Solution :

Let x be the number of miles driven.

First car company charges :

34 per day and 0.50 every mile driven

= 34 + 0.50x

Second car company charges :

= 20 per day and 0.75 every mile drive,

= 20 + 0.75x

Both company should have the same charge.

34 + 0.50x = 20 + 0.75x

34 - 20 = 0.75x - 0.50x

14 = 0.25x 

x = 14/0.25

x = 56

So, 56 miles is driven.

Problem 8 :

The table shows the number of hours Jake studied for his math tests and his corresponding grade.

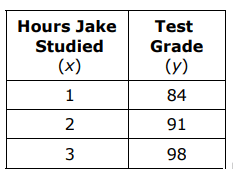
Another student, Howie, increased his test scores 6 points for each hour he studied. Which statement correctly describes the rate of change between hours studied and corresponding test scores of the two students?

A) Jake’s test scores increased by 1 point more than Howie’s test scores for each hour studied.

B) Jake’s test scores increased by 3 points more than Howie’s test scores for each hour studied.

C) Howie’s test scores increased by 1 point more than Jake’s test scores for each hour studied.

D) Howie’s test scores increased by 3 points more than Jake’s test scores for each hour studied.

Solution :

Rate of change of Jake :

Rate of change of Howie :

6 (given)

Jake’s test scores increased by 1 point more than Howie’s test scores for each hour studied.

So, option A is correct.

Problem 9 :

A group of students were asked if they are in the Math Club and if they are in the Literature Club. Partial results are shown in the table.

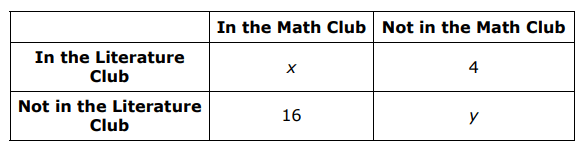
• Of the students in the Math Club, 67% (rounded) are not in the Literature Club.
• Of the students not in the Math Club, 78% (rounded) are not in the Literature Club.

What is the value of x + y?

A)    22       B)  24        C)  42         D)  66

Solution :

67% are not in the Literature Club. Number of students are not in Litreature Club = 4

67% of total students = 16

0.67(total students) = 16

Total students = 16/0.67

 = 23.8

Total students = 24

x = 24 - 16

x = 8

78% are not in the Litreature Club , 22% are in Litreature Club.

22% of total students = 4

0.22(total students) = 4

Total students = 4/0.22

Total students = 18

y = 18 - 4.

y = 14

x + y = 8 + 14

= 22

Problem 10 :

Dennis compared the y-intercept of the graph of the function

f(x) = 3x + 5

to the y-intercept of the graph of the linear function that includes the points in the table below.

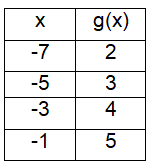
What is the difference when the y-intercept of f(x) is subtracted from y-intercept of g(x) ?

a)  11.0      b)  9.3        c)  0.5       d)  5.5

Solution :

f(x) = 3x + 5

y-intercept of f(x) = 5

From the table, choosing two points from the table (-7, 2) and (-1, 5).

Slope = (y₂ - y₁)/(x₂ - x₁)

= (5 - 2) / (-1 + 7)

= 3/6

= 1/2

Equation of the line :

(y - y₁) = m(x - x₁)

y - 5 = 1/2(x + 1)

When x = 0, y = 1/2 + 5 ==>  5.5

Difference between y-intercepts

= y-intercept of g(x) - y-intercept of f(x) 

= 5.5 - 5

= 0.5

Problem 11 :

Lucy and Barbara began saving money in the same week. The table below shows the models for the amount of money Lucy and Barbara has saved after x weeks.

After how many weeks will Lucy and Barbara have the same amount of money saved ?

a)  1.1 weeks      b)  1.7 weeks     c)  8 weeks     d)  12 weeks

Solution :

f(x) = 10x + 5 -----(1)

g(x) = 7.5x + 25  -----(2)

(1) = (2)

10x + 5 = 7.5x + 25

10x - 7.5x = 25 - 5

2.5x = 20

x = 20/2.5

x = 8

So, 8 weeks.