LINE DRAWN FROM THE CENTER TO TANGENT

A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90˚.

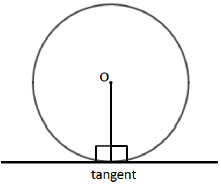
• The line which is drawn from the center of the circle to tangent of that circle is simply known as the radius of that circle.
• The radius will be perpendicular on the tangent in this case.
• The radius is the half of the diameter of the same circle.

Problem 1 :

Length of the tangent is 8 cm, radius of the circle is 6 cm. Find the distance from center to the point away from the circle.

(a) 10 cm        (b) 5 cm      (c) √7 cm      (d) 2√7 cm

Solution :

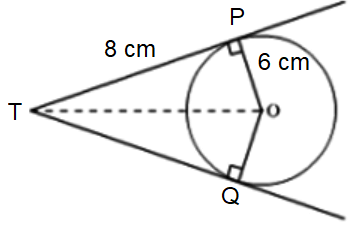
OP is perpendicular to TP.

TO² = TP² + OP²

TO² = 8² + 6²

TO² = 64 + 36

TO² = 100

TO = √100

TO = 10 cm

Problem 2 :

If tangents PA and PB from a point P to a circle with center O are inclined to each other at an angle of 80°, then ∠POA is

(a) 30⁰        (b) 60⁰      (c) 50⁰      (d) 100⁰

Solution :

OA is perpendicular to AP.

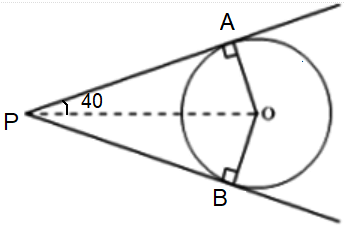
∠POA = ?

∠POA + ∠APO + ∠PAO = 180

∠POA + 40 + 90 = 180

∠POA + 130 = 180

∠POA = 180 - 130

∠POA = 50

Problem 3 :

If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm then length of each tangent is --------------

Solution :

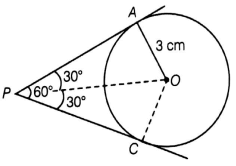
OA is perpendicular to PA. To find the length of tangent PA, we use 

tan θ = Opposite side/Adjacent side

tan 30 = OA/PA

1/√3 = 3/PA

PA = 3√3

Problem 4 :

If the angle between two tangents drawn from a point T to a circle of radius r and center O is 120⁰ then find the length of TP .

Solution :

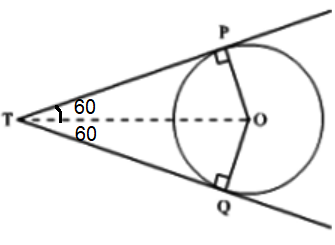
OA is perpendicular to PA. To find the length of tangent PA, we use 

tan θ = Opposite side/Adjacent side

tan 60 = OP/TP

√3 = r/TP

TP = r/√3

Problem 5 :

The length of a tangent from a point A at distance 5 cm from the center of the circle is 4 cm. Find the radius of the circle.

(a) 4 cm      (b) 3 cm      (c) 6 cm       (d) 5 cm

Solution :

Length of tangent = 4 cm

Distance from the point away from the circle to center = 5 cm

The line drawn from center to tangent must be a perpendicular.

5² = 4² + r²

25 = 16 + r²

r² = 25 - 16

r² = 9

r = 3 cm

Problem 6 :

PQ is a chord of length 8 cm of a circle of radius 5 cm .The tangents at P and Q intersect at a point T . Find the length TP.

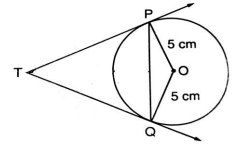
Solution :

Length of PQ = 8 cm, when we draw the perpendicular from O to PQ, it will be a perpendicular bisector.

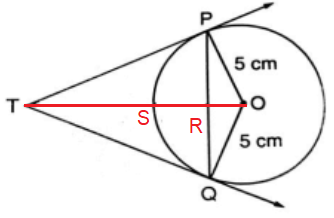
The midpoint of PQ be C.

PO² = OR² + RP²

5² = OR² + 4²

25 - 16 = OR²

OR² = 9

OR = 3

In triangle TPR,

TP² = TR² + RP²

OS = 5 cm, OS = SR + RO

5 = SR + 3

SR = 2, let TS = x and TP = y

y² = (2 + x)² + 4²

y² = 2² + 2(2)x + x² + 4²

y² = x² + 4x + 20  -----(1)

In triangle TPO

TO² = TP² + OP²

(5 + x)² = y² + 5²

25 + x² + 10x = y² + 25

y² = x² + 10x  -----(2)

(1) = (2)

x² + 4x + 20 = x² + 10x

6x = 20

x = 5/3

By applying the value of x in (2), we get

y² = (5/3)² + 10(5/3) 

y² = 25/9 + 50/3

y² = (25+150)/9

y² = 175/9

y = 4.40 cm

So, length of tangent TP is 4.40 cm.