LENGTH OF TANGENT TO CIRCLE FROM AN EXTERNAL POINT

Tangents from an external point are equal in length.

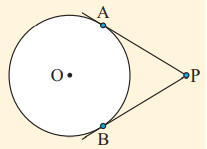
AP = PB

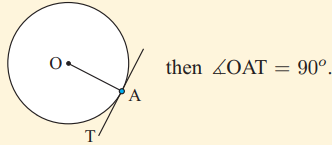
The tangent to a circle is perpendicular to the radius at the point of contact.

Problem 1 :

PT is a tangent to the circle with centre O. If OT = 6 cm & OP = 10 cm, then length of tangent PT is

(a) 8 cm    (b)12 cm    (c) 10 cm   (d) 16 cm

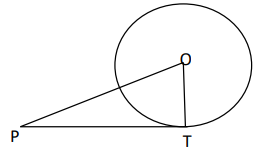
Solution :

PO² = OT² + PT²

10² = 6² + PT²

PT² = 100 - 36

PT² = 64

PT = 8 cm

So, the length of the tangent is 8 cm.

Problem 2 :

AP & AQ are tangents are tangents from a point A to a circle with centre O & radius 9 cm. If OA = 15cm, then find AP + AQ

Solution :

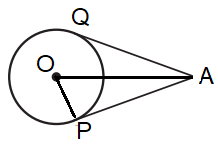
OP = 9 cm, OA = 15 cm

OA² = OP² + PA²

15² = 9² + PA²

225 - 81 = PA²

PA² = 144

PA = 12

Length of the tangents drawn from the external point to the point of contact will be equal.

PA = AQ = 12

AP + AQ = 24 cm

Problem 3 :

In the figure given below, AC, AD and AB are tangents. If AB = 5 cm, find AD.

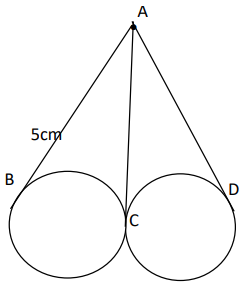
Solution :

From the picture given, it is clear AB and AC will have same measure, because these are the tangents drawn from the external point of the circle.

AB = AC = 5 cm

AC and AD are the tangents drawn from external point of the circle.

AC = AD = 5 cm

So, the length of AD is 5 cm.

Problem 4 :

Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.

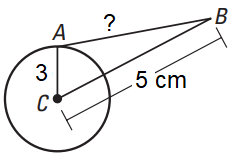
Solution :

AB = Length of tangent.

BC² = AC² + AB²

5² = 3² + AB²

25 - 9 = AB²

AB² = 16 

AB = 4

Problem 5 :

A point P is at a distance 13 cm from the centre C of a circle and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.

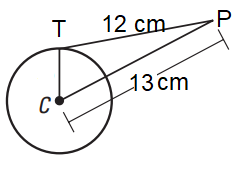
Solution :

Let x be the radius of the circle. Then r = CT

CP² = CT² + TP²

13² = x² + 12²

169 - 144 = x²

x² = 25

x = 5

Problem 6 :

From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre of the circle is 25 cm. Find the radius of the circle

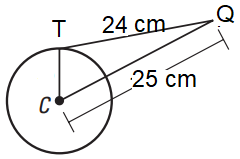
Solution :

Let x be the radius of the circle. Then r = CT

CQ² = CT² + TQ²

25² = r² + 24²

625 = r² + 576

r² = 625 - 576

r² = 49

r = 7 cm

So, the radius of the circle is 7 cm.

Problem 7 : 

The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle

Solution :

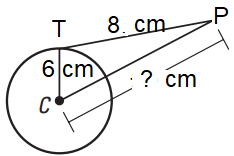
CP² = CT² + TP²

CQ² = 6² + 8²

CQ² = 100

CQ = 10 cm

So, the distance of p from the center of the circle is 10 cm.

Problem 8 :

Find x.

Solution :

(x + 2)² = (x - 6)² + (x + 1)²

x² + 4x + 4 = x² - 12x + 36 + x² + 2x + 1

2x² - x² - 10x - 4x + 37 - 4 = 0

x² - 14x + 33 = 0

(x - 11)(x - 3) = 0

x = 11 and x = 3

Problem 9 :

Triangle ABC is circumscribed, find the value of x.

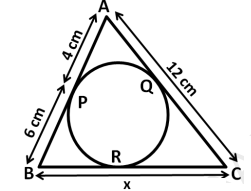
Solution :

AP = AQ = 4 cm

BP = BR = 6 cm

AC = 12 cm

AQ + QC = 12

4 + QC = 12

QC = 8 cm = CR

BC = x

BR + RC = x

6 + 8 = x

x = 14 cm