LAW OF SINES TO FIND MISSING SIDE

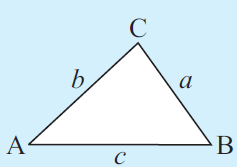
The sine rule is a set of equations which connects the lengths of the sides of any triangle with the sine of the opposite angles.

The triangle does not have to be right angled for sine rule to be used.

In any triangle ABC, with sides a, b and c units in length and opposite sides A, B and C respectively.

Solve for the unknown in each triangle. Round to the nearest tenth.

Problem 1 :

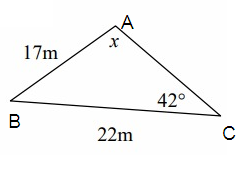
Solution:

From the picture given above, we know that we need to find the angle A.

BC = a = 22 m, AB = c = 17 m and AC = b 

∠C = 42°

Problem 2 :

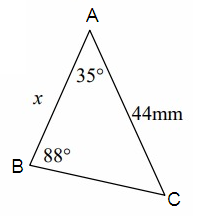
Solution:

AC = b = 44 mm, AB = c = x, BC = a

∠A = 35°, ∠B = 88°

Here, 

∠C = 180° - (35° + 88°)

∠C = 57°

Problem 3 :

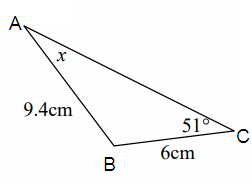
Solution:

AB = c = 9.4 cm, BC = a = 6 cm, AC = b

∠C = 51°

Problem 4 :

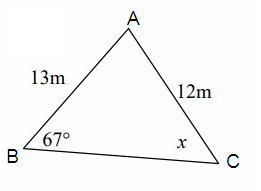
Solution:

AC = b = 12 m, AB = c = 13 m, BC = a

∠B = 67° 

Problem 5 :

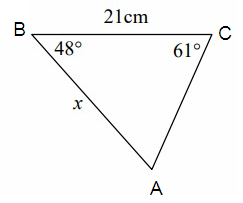
Solution:

AB = c = x, BC = a = 21 cm, AC = b

∠B = 48°, ∠C = 61°

∠A = 180° - (48° + 61°)

∠A = 71°

Problem 6 :   

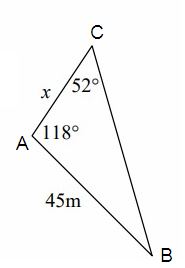
Solution:

AB = c = 45 m, AC = b = x, BC = a

∠A = 118°, ∠C = 52°

∠B = 180° - (118° + 52°)

∠B = 10°