LAW OF SINES TO FIND ALL MISSING SIDES AND ANGLES

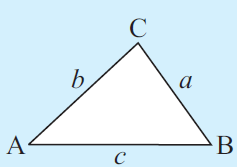
Solve for all missing sides and angles in each triangle. Round to the nearest tenth.

Problem 1 :

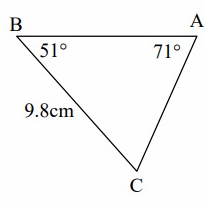
Solution:

AB = c, AC = b, BC = a = 9.8 cm

∠A = 71, ∠B = 51

Find b :

In triangle ABC,

∠A + ∠B + ∠C = 180

71 + 51 + ∠C = 180

∠C = 180 - 122

∠C = 58

Find c :

Hence the missing sides and missing angles are 8.05 cm, 8.79 cm and 58º respectively.

Problem 2 :

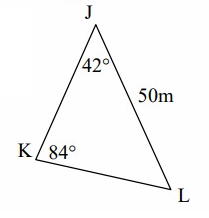
Solution:

JL = 50 m, ∠J = 42º, ∠K = 84º

Find j :

In triangle JKL,

∠J + ∠K + ∠L = 180

42 + 84 + ∠L = 180

∠L = 180 - 126

∠L = 54

Find l :

Hence the missing sides and missing angles are 33.65 m, 40.7 m and 54º respectively.

Problem 3 :

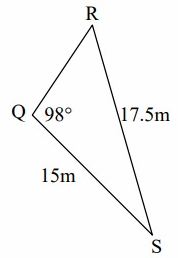
Solution:

RQ = s, QS = r = 15 m, RS = q = 17.5 m

∠Q = 98º

Find ∠R :

In triangle QRS,

∠Q + ∠R + ∠S = 180

98 + 58.1 + ∠S = 180

∠S = 180 - 156.1

∠S = 23.9

Find s :

Hence the missing sides and missing angles are 7.16 m and 58.1º, 23.9º respectively.

Problem 4 :

Solution:

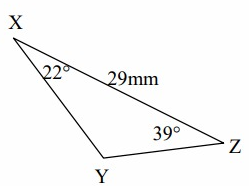
XZ = y = 29 mm, XY = z,  YZ = x

∠X = 22º, ∠Z = 39º

In triangle XYZ,

∠X + ∠Y + ∠Z = 180

22 + ∠Y + 39 = 180

∠Y = 180 - 61

∠Y = 119

Find x :

Find z :

Hence the missing sides and missing angles are 12.4 mm, 20.9 mm and 119º respectively.

Problem 5 :

Solution:

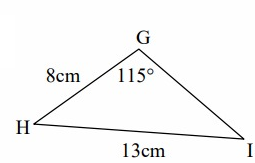
GH = i = 8 cm, HI = g = 13 cm, GI = h

∠G = 115º

Find ∠I :

In triangle GHI,

∠G + ∠H + ∠I = 180

115 + ∠H + 33.9 = 180

∠H = 180 - 148.9

∠H = 31.1

Find h :

Hence the missing sides and missing angles are 7.4 cm and 31.1º, 33.9º respectively.

Problem 6 :

Solution:

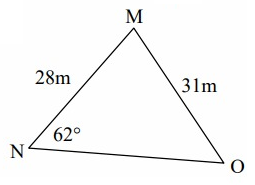
MN = o = 28 m, MO = n = 31 m, No = m

∠N = 62º

In triangle MNO,

∠M + ∠N + ∠O = 180

∠M  + 62 + 52.9 = 180

∠M = 180 - 114.9

∠M = 65.1

Find m :

Hence the missing sides and missing angles are 31.8 m and 65.1º, 52.9º respectively.