LATERAL SURFACE AREA AND TOTAL SURFACE AREA OF TRIANGULAR PRISM

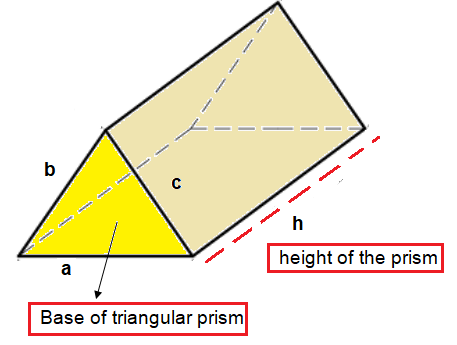
Lateral surface area = ph

p = Perimeter of the triangle and h = height of the prism

Total surface area = ph + 2B

B = Base area of triangular prism

Problem 1 :

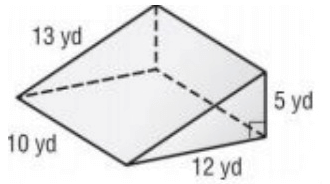
Find the lateral surface area and total surface area of the triangular prism.

Solution :

Lateral surface area = p × h

P - Perimeter of base

= 12 + 13 + 5

= 30

Lateral surface area = 30 × 10

= 300 yd² --- > (1)

Total surface area = ph + 2B

Area of triangle = 1/2 × b × h

= 2 × 1/2 × 12 × 5

= 60 yd² --- > (2)

Add (1) & (2)

= 300 + 60

Total surface area   = 360 yd²

Problem 2 :

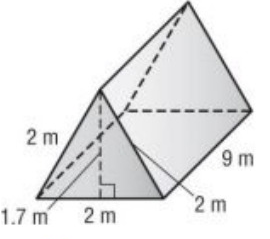
Find the lateral surface area and total surface area of the triangular prism.

Solution :

Area of triangle = 2(1/2) × b × h

= 2(1/2) × 2 × 1.7

= 3.4 m² --- > (1)

Area of rectangle = 3 ×b × h

= 3 × 9 × 2

= 54 m² --- > (2)

Add (1) & (2)

Surface area = 3.4 + 54

= 57.4 m²

So, surface area of the triangular prism = 57.4 m²

Problem 3 :

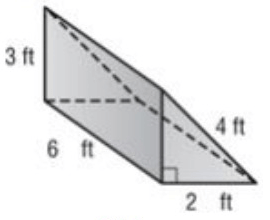
Find the lateral surface area and total surface area of the triangular prism.

Solution :

Lateral surface area = p × h

P - Perimeter of base       

= 3 + 2 + 4

= 9

Lateral surface area = 9 × 6

= 54 ft² --- > (1)

Total surface area = ph + 2B

Area of triangle = 1/2 × b × h

= 2 × 1/2 × 2 × 3

= 6 ft² --- > (2)

Add (1) & (2)

= 54 + 6

Total surface area   = 60 ft²

Problem 4 :

Determine the surface area of the tent. The front of the tent has the shape on an isosceles triangle.

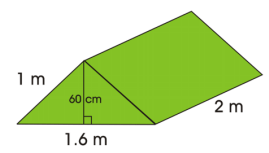
Solution :

Lateral surface area = p × h

P - Perimeter of base       

= 1.6 + 1 + 1

= 3.6

height of the prism = 2 m

Lateral surface area = 3.6 × 2

= 7.2 m²

Problem 5 :

This A-frame chalet needs to have the roof shingled. Determine the surface area of the roof.

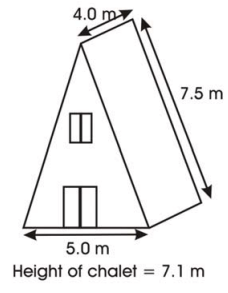
Hint: Think about whether the height of the chalet is the same as the height of the prism. Which measurements are unnecessary for this question?

Solution :

Surface area of roof = p × h

p = perimeter

= 5 + 7.5 + 7.5

= 20 m

Length from one end of the triangular face to another end is 4 m.

Surface area of roof = 20 x 4

= 80 square meter

Problem 6 :

Hector is designing a glass greenhouse for a city park. He has a 40-foot by 20- foot rectangular plot available. He wants the roof to be a triangular prism in which the center of the roof is 4 feet higher than the edges. 

The glass costs $25 per square foot, and Hector cannot spend more than $60,000 on glass.

a) What is the maximum height that Hector should make the edge of the roof?

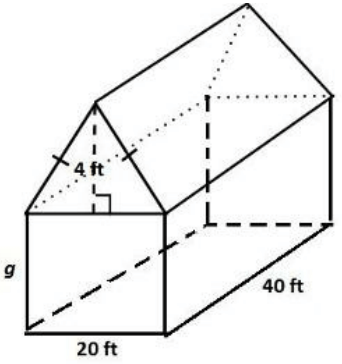
Solution :

In the triangular shape, the slant height :

l² = 4² + 10²

l² = 16 + 100

l = √116

l = 10.77

Find the sum of the surface areas of each individual section. 

The rectangular section of the front and back

= 2 × 20 × g or 40g ft²

The sides cover 

= 2 × 40 × g

= 80g ft²

The triangular tops of the front and back of the greenhouse cover

= 2(0.5)(4)(20) or 80 ft²

Thus, the roof covers 

= 2(40)(10.77) or 861 ft²

The total surface area is

= 861 + 80 + 120g ft²

Hector can use up to 60,000 ÷ 25 or 2400 ft²

941 + 120g = 2400

120g = 1459

g = 12.1

Therefore, g is approximately 12.1

Problem 7 :

A solid glass paperweight is in the shape of a triangular prism The density of the glass is 2.4 g/cm³ Work out the mass of the paperweight.

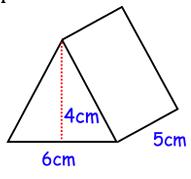
Solution :

Base area of triangle = (1/2) x base x height

= (1/2) x 6 x 4

= 12 cm²

Height of the triangular prism = 5 cm

Volume of the triangular prism = base area x height

= 12 x 5

= 60 square cm

Density of glass = 2.4 g/cm³

Mass of the paper weight = 60 x 2.4

= 144 grams

Problem 8 :

A triangular prism has a rectangular prism cut out of it from one base to the opposite base, as shown in the figure. Determine the volume of the figure, provided all dimensions are in millimeters.

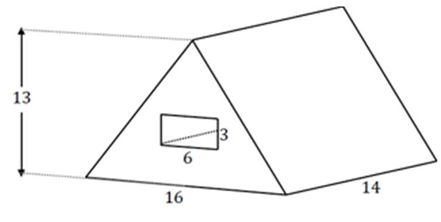
Solution :

Dimension of triangular prism :

Base = 16 mm, height of triangle = 13 mm and height of triangular prism = 14 mm

Dimension of rectangular prism :

length = 6 mm, width = 3 mm and height = 14 mm

Volume of figure = Volume of triangular prism - volume of rectangular prism

= (1/2) x 16 x 13 x 14 - 6 x 3 x 14

= 8 x 13 x 14 - 6 x 3 x 14

= 1456 - 252

= 1204 mm²

Problem 9 :

Find the volume of the right triangular prism.

a. 60 u³      b. 100 u³      c. 120 u³       d. 200 u³

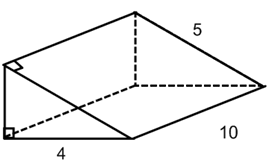
Solution :

Base of the triangle = 4 units

Slant height of the triangle = 5 units

Let x be the height of the triangle.

Using Pythagorean theorem,

x² = 5² - 4²

x² = 25 - 16

= 9

x = 3 units

Height of the triangular prism = 10 units

Volume of triangular prism = base area x height

= (1/2) x 4 x 3 x 10

= 2 x 3 x 10

= 60 cubic units

So, the volume of the triangular prims is 60 cubic units which is option a