INTERSECTING SECANTS THEOREM

The measure of an angle formed by two secants, a secant and a tangent, or two tangents intersecting in the exterior of a circle is equal to one-half the positive difference of the measures of the intercepted arcs.

Problem 1 :

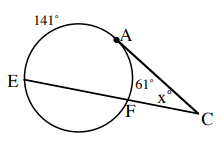
Solution :

x = (1/2) [141 - 61]

x = (1/2) (80)

x = 40

Problem 2 :

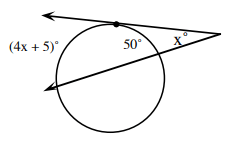
Solution :

x = (1/2) [4x + 5 - 50]

x = (1/2) (4x - 45)

Multiplying by 2 on both sides

2x = 4x - 45

2x - 4x = -45

2x = 45

x = 22.5

Problem 3 :

Two secants drawn to a circle from an external point P intercept arcs of 90° and 20° on the circle. Find measure of angle P.

Solution :

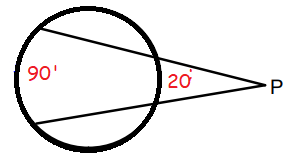
Angle p = (1/2)(90 - 20)

= (1/2) (70)

p = 35

Problem 4 :

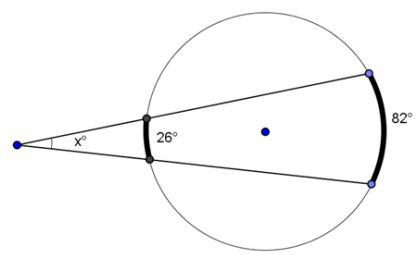
Solution :

x = (1/2)(82 - 26)

= (1/2) (56)

x = 28

Problem 5 :

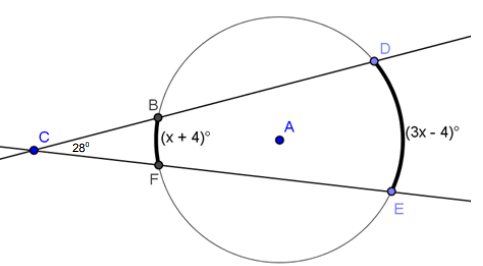
Solution :

28 = (1/2)( 3x - 4 - (x + 4) )

28 = (1/2)(3x - 4 - x - 4)

28 = (1/2)(2x - 8)

28 = (1/2) 2(x - 4)

28 = x - 4

28 + 4 = x

x = 32

Problem 6 :

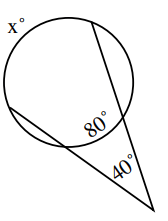
Solution :

40 = (1/2)(x - 80)

Multiplying by 2 on both sides

80 = x - 80

Adding 80 on both sides.

x = 80 + 80

x = 160

Problem 7 :

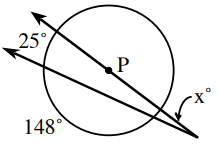
Solution :

Since P is the center, the line passing through the center will divide the circle into two equal parts. Hence it is semi circle.

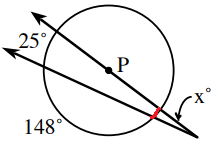
Let t be the angle measure intercepted by the smaller arc.

148 + 25 + t = 180

173 + t = 180

t = 180 - 173

t = 7

x = (1/2) (25 - 7)

x = (1/2)(18)

x = 9

Problem 8 :

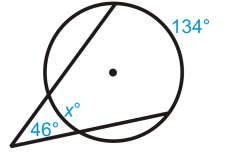
Solution :

46 = (1/2)(134 - x)

Multiplying by 2 on both sides.

46(2) = 134 - x

92 = 134 - x

Subtracting 134 and adding x on both sides.

92 - 134 = -x

x = 42

Problem 9 :

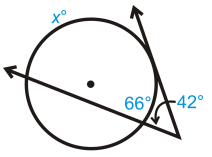
Solution :

42 = (1/2)(x - 66)

Multiplying by 2 on both sides.

42(2) = x - 66

84 = x - 66

Adding 66 on both sides.

x = 84 + 66

x = 150

Problem 10 :

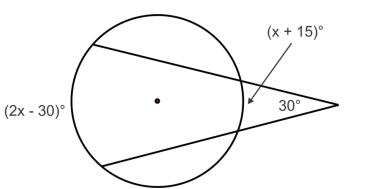
Solution :

30 = (1/2)( 2x - 30 - (x + 15) )

30 = (1/2)(2x - 30 - x - 15)

30 = (1/2)(x - 45)

Multiplying by 2 on both sides.

60 = x - 45

x = 60 + 45

x = 105

Problem 11 :

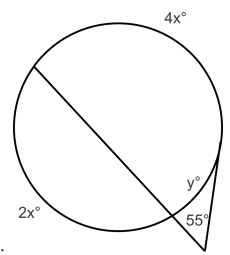
Solution :

55 = (1/2)(4x - y)

Multiplying by 2 on both sides.

110 = 4x - y

y = 4x - 110  -----(1)

2x + 4x + y = 360

6x + y = 360 -----(2)

Applying (1) in (2), we get

6x + 4x - 110 = 360

10x - 110 = 360

add 110 on both sides

10x = 360 + 110

10x = 470

x = 47

Applying the value of x in (1), we get

y = 4(47) - 110

y = 188 - 110

y = 78