INTREPRETING LINEAR FUNCTIONS WORD PROBLEMS

Example 1 :

The function below shows the cost of a hamburger with different numbers of toppings (t).

f(t) = 1.90 + 1.40t

a) What is the y-intercept, and what does it mean?

b) What is the slope, and what does it mean?

c) If Jodi paid $3.30 for a hamburger, how many toppings were on Jodi’s hamburger?

Solution :

f(t) = Cost of hamburger and t = number of toppings.

(a) f(t) = 1.40t + 1.90

To find y-intercept, we will apply t = 0

f(0) = 1.40(0) + 1.90

f(0) = 1.90

When there is zero topping the cost of hamburger is $1.90

b) By comparing the given equation with y = mx + b, we get slope = 1.40

Here the meaning of slope is how the charge is being affected for every increase of one topping.

c) f(t) = 1.40t + 1.90

Cost of hamburger f(t) = 3.30

3.30 = 1.40t + 1.90

Subtracting 1.90 on both sides.

3.30 - 1.90 = 1.40t

1.4 = 1.40t

t = 1.4/1.40

t = 1

So, there is one topping.

Example 2 :

The function below shows the cost of an ice cream sundae with different numbers of toppings (t).

f(t) = 2.25 + 0.75t

a) What is the y-intercept, and what does it mean?

b) What is the slope, and what does it mean?

Solution :

f(t) = 2.25 + 0.75t

a) To find y-intercept, we have to apply t = 0

f(0) = 2.25 + 0.75(0)

f(0) = 2.25

When there is no topping, the cost of ice cream sundae is $2.25.

b) By comparing the given equation with y = mx + b, we get slope = 0.75

Here the meaning of slope is how the charge is being affected for every increase of one topping.

For every one increase of topping, we have to pay 0.75 more.

Example 3 :

The graph below shows the number of newspapers delivered and total pay for Leona’ newspaper delivery job. What does the slope ?  

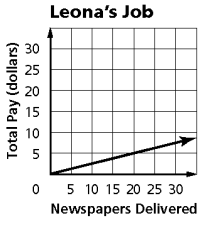
Solution :

x-axis ==> Newspaper delivered

y-axis ==> Total pay

Taking two points on the line (0, 0) ad (20, 5)

Slope = (y₂ - y₁)/(x₂ - x₁)

m = (5 - 0)/(20 - 0)

m = 1/4

Example 4 :

Dionne pays a fixed fee plus an hourly rate to rent a boat. The table below shows how much Dionne paid for the boat. What was Dionne’s hourly rate to rent the boat?

Solution :

Writing it as ordered pairs, we get

(1, 27) and (2, 39)

Slope = (y₂ - y₁)/(x₂ - x₁)

m = (39 - 27)/(2 - 1)

m = 12/1

m = 12

Equation of linear function y = 12x + b

To find fixed cost, we can apply one of the points from the table.

Applying (3, 51), we get

51 = 12(3) + b

51 = 36 + b

b = 51 - 36

b = 15

So, hourly rate is $12.

Example 5 :

Colby put $100 in a savings account. The graph below shows  how the amount in the account would increase over the next ten years. What does the y-intercept represent? 

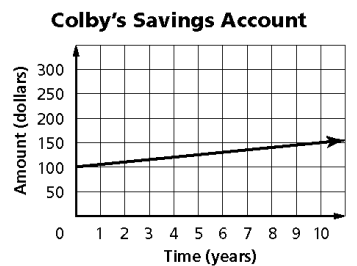
Solution :

By observing the graph, y-intercept is 100.

When time is 0, the amount in savings account is $100.

Example 6 :

Tara pays a base rate for her long distance phone service plus a per-minute charge. The graph below shows what she would pay for her long distance phone service for the first 60 minutes. What does the y-intercept of this graph represent? 

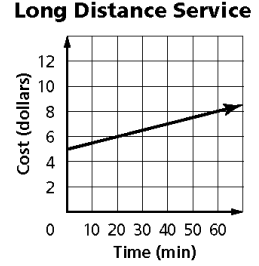
Solution :

By observing the graphing, y-intercept is 5.

The base rate is $5.

Example 7 :

Rich is a member of a gym. He pays a monthly fee plus a per-visit fee. The equation below represents the monthly amount Rich pays for his membership to the gym per month for x visits.

y = 3x + 10

What does the y-intercept of the graph of this equation represent?

Solution :

By comparing the given equation with y = mx + b, we get

slope = 3 and y-intercept = 10

So, membership of the gym is $10 and per visit he has to pay $3.