INTERPRETING BOX AND WHISKER PLOTS

A box and whisker plot (or simply box plot) is a visual display of the descriptive statistics of a data set. It shows 

• Minimum value 
• The lower quartile (Q₁)
• the median (Q₂)
• the upper quartile (Q₃)
• the maximum value

These five numbers form what is known as the five number summary of a data set

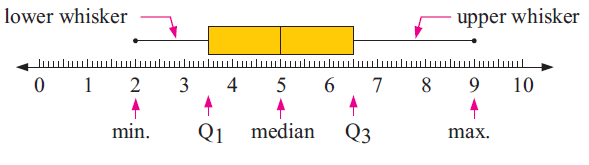
• The rectangular box represents the "middle" half of the data set.
• The lower whisker represents the 25% of the data with smallest values.
• The upper whisker represents the 25% of the data with greatest values.
  

How to calculate median ?

The median(Q₂) which divides the data into two equal parts.

Calculating Q1 :

Calculate the lower quartile (Q₁) by finding the median of lower half.

Calculating Q3 :

Calculate the upper quartile (Q₃) by finding the median of upper half.

Calculating Range :

Range = Greatest value - smallest value

Calculating interquartile range :

Interquartile range = Q₃ - Q₁

Problem 1 :

The accompanying box and whisker plot represents the cost, in dollars of the twelve CD's ?

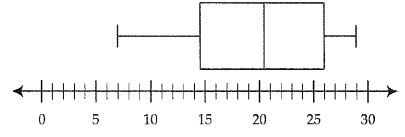
1)  What is the upper quartile ?

2) What is the range of the costs of the CD's ?

3)  What is the median ?

4)  Which cost represents the 100th percentile ?

5)  How many CD's cost between $14.50 and $26.00 ?

6)  How many CD's cost less than $14.50 ?

Solution :

1)  Upper quartile (Q3) = 26

2) Range = Largest value - smallest value

= 29 - 7

= 22

3)  median = 20.5

4)  100th percentile (maximum value) = 29

5) Total number CD's = 12 (given)

50% of the CD's cost between $14.50 and $26.00

Number of CD's in between the above cost = 50% of 12

= 6 CD's

6) 25% of CD's cost less than $14.50

= 25% of total number of CD

= 0.25 (12)

= 3

Problem 2 :

What is the median price for a snowboard at Middle snow boards ?

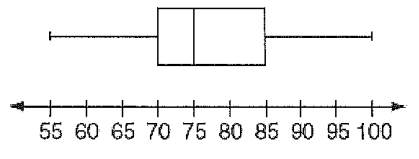
1)  What is the median score ?

a)  70      b)  75     c)  77      d)  85

2)  What is the interquartile range ?

Solution :

1)  Median score = 75

2) Interquartile range = Q3 - Q1

= 85 - 70

= 15

Problem 3 :

What is the value of the third quartile shown on the box and whisker plot below ?

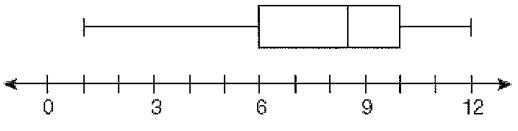
a)  6      b)  10     c)  8.5      d)  12

Solution :

Third quartile (Q3) = 10

Problem 4 :

A movie theater recorded the number of tickets sold daily for a popular movie during the month of June. The box and whisker plot shown below represents the data for the number of tickets sold, in hundreds.

Which conclusion can be made using this plot ?

a) The second quartile is 600.

b)  The mean of the attendance is 400.

c) The range of the attendance is 300 to 600.

d) 25% of the attendance is between 300 and 400.

Solution :

a) The second quartile is 400 (Given is 600). So it is incorrect.

b)  Median is 400 (Given as mean). So, it is incorrect.

c)  Range = 900 - 100

= 800

Given is between 300 to 600. So, it is incorrect.

d)  25% of the attendance is between 300 and 400.

Problem 5 :

The accompanying box and whisker plots can be used to compare the annual incomes of three professions.

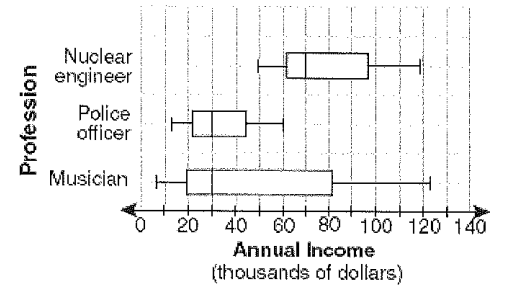
Based on the box and whisker plots, which statement is true ?

a) The median income of nuclear engineers is greater than the income of all musicians.

b)  The median income for police officers and musicians is the same.

c)  All nuclear engineers earn more than all police officers.

d)  A musician will eventually earn more than a police officer.

Solution :

By observing the box plot, it is clear median income of police officers and musicians is the same. So, option b is correct.

Problem 6 :

The data set 5, 6, 7, 8, 9, 9, 9, 10, 12, 14, 17, 17, 18, 19, 19 represents the number of hours spent on the internet in a week by students in mathematics class. Which box and whisker plot represents the data ?

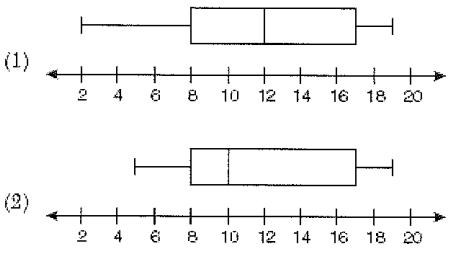
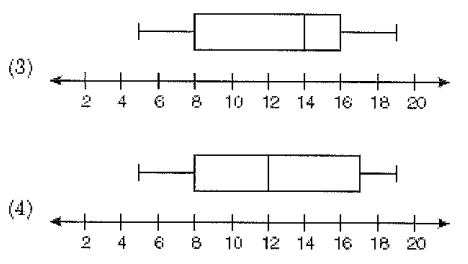
Solution :

5, 6, 7, 8, 9, 9, 9, 10, 12, 14, 17, 17, 18, 19, 19

Minimum value = 5

Total number of terms = 15, dividing into two parts.

5, 6, 7, 8, 9, 9, 9, 10, 12, 14, 17, 17, 18, 19, 19

Q2 = 10

Median of lower quartile :

5, 6, 7, 8, 9, 9, 9,

Q1 = 8

Median of upper quartile :

12, 14, 17, 17, 18, 19, 19

Q3 = 17

Maximum value = 19

So, option (2) is correct.

Problem 7 :

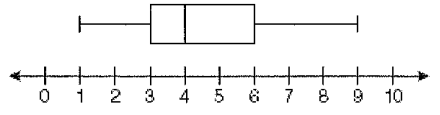
Using the plot given below, find

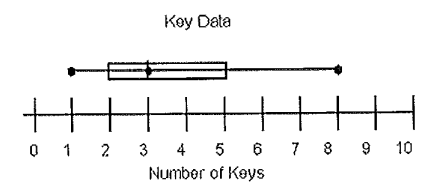
1) Range

2)  IQR

3)  Percent more than 5

4)  Percent at least 2

5)  If there are 32 numbers in the data set, how many are less than 3 ?

Solution :

1) Range = maximum value - minimum value

= 8 - 1

= 7

2) IQR = Q3 - Q1

= 5 - 2

= 3

3)  25% are more than 5

4)  75% are at least 2.

5)  From the box plot, 50% are lesser than 3.

= 50% of 32 

= 0.50(32)

= 16

Problem 8 :

Using the plot given below, find

the percentage of data values less than 7.

Solution :

75% of the data values are less than 7.