INTERPRETING BAR GRAPHS

Example 1 :

The bar graph shows the number of different items sold in an electrical goods store in a given month.

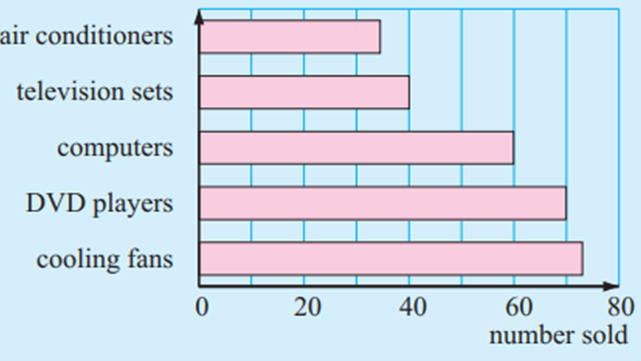
(a)  How many DVD players were sold for the month ?

(b) How many more computers were sold than television sets ?

(c)  What percentage of the items sold were cooling fans ?

Solution :

(a)  By observing the bar graph, 70 DVD players were sold for the month.

(b)  60 computers were sold out.

(c)  Number of air conditioners sold = 34

Number of television sets = 40

Number of computer sets = 60

DVD players = 70

Cooling fans = 73 

Total = 34 + 40 + 60 + 70 + 73

= 277

Percentage of cooling fans = (73/277) x 100%

= 26.53%

= 27%

Example 2 :

(a)  Estimate the median house price in 2008 in

(i) London

(ii) Liver pool

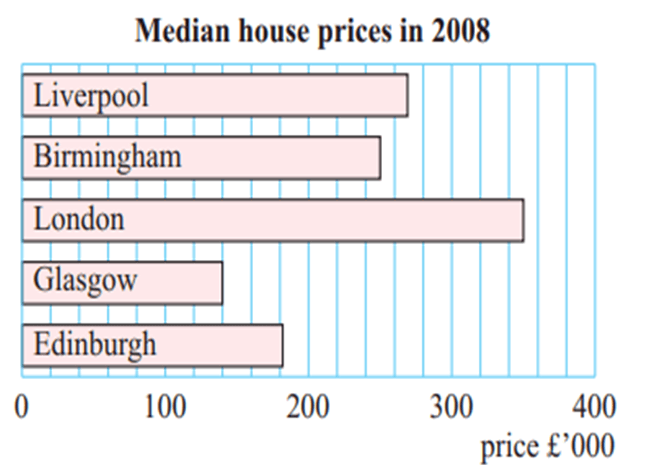
(b)  How much bigger is the median house price in Edinburgh than Glasgow ?

(c)  What percentage is the median Birmingham price of the median Liverpool price in the year 2008?

Solution :

(a)  (i)  length of bar of London = 353

Median price = 353 x 1000 ==>  353000

(ii)  Liver pool = 278

Price = 278 x 1000 ==> 278000

(b)  Price in Edinburg = 183 x1000 ==>  183000

Price in Glasgow = 140 x 1000 ==> 140000

Difference = 183000 - 140000

= 43000

(c)  Price in Birmingham = 250000

Price in liver pool = 270000

Percentage = (250000/270000) x 100%

= 92.59%

Approximately 93%.

Example 3 :

The graph along side displays the result of a national phone in of children ages six to sixteen as to what they do at home between 3 pm to 6 pm

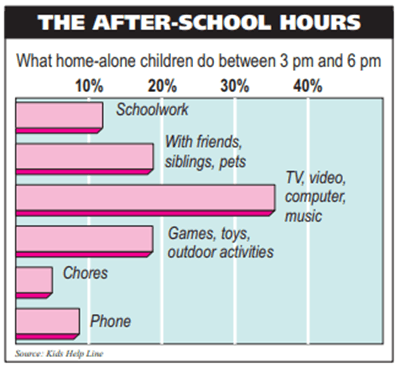
(a)  Use the graph to determine the percentage of children who.

(i) Watch TV, videos, play with computers or listen to music.

(ii)  Spend time with friends, siblings or pets.

(b) If 240 children were surveyed.

(i) How many do school work ?

(ii)  How many spend more time on the phone rather than do chores ?

Solution :

(a)  (i) 35% of children who watch TV, videos, play with computers or listen to music.

(ii)  Which is closer to 20%, so 19% o children spend time with friends, siblings or pets.

(b)  Number of children surveyed = 240

Number of children do school work = 12% of 240

= 0.12 (240)

= 28.8

So, 29 children do their school work.

(ii) Children spend time on phone = 9%

Number of children spend time on phone = 0.09(240)

= 21.6 approximately 22

Children spend time Chores = 5%

Number of children spend time on chores = 0.05(240)

= 12

= 22 - 12

= 10 children

Example 4 :

The bar graphs shows the crude oil reserves for the top five oil producing countries in the world.

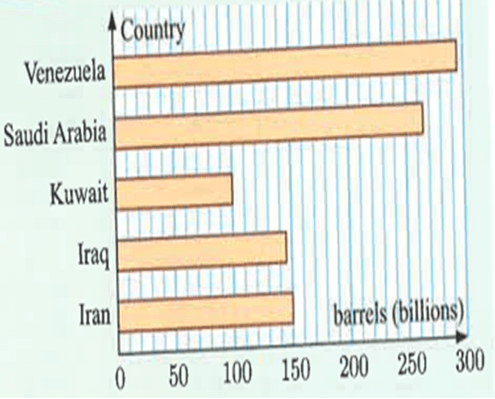
(a) How many billion barrels of crude oil do these countries have in total ?

(b) How many more barrels can Saudi Arabia produce than Iraq?

(c) What percentage of the crude oil is held by Iran ?

Solution :

Iran = 150, Iraq = 145, Kuwait = 100, Saudi Arabia = 255, Venezuela = 295

Total = 150 + 145 + 100 + 265 + 295

= 955

So, 955 barrels are in total.

(b)  Number of barrels produced by Iraq = 145

Number of barrels produced by Saudi Arabia = 255

Difference = 255 - 145 ==> 110

So, Saudi Arabia has produced 110 more barrels than Iraq. 

(c)  Quantity of Crude oil produced in Iran = 150

Percentage = (150/955) x 100%

= 15.70% 

So, 15.7% of crude oil produced by Iran.