INTERIOR ANGLES OF A QUADRATILATERAL

A quadrilateral is a four sided polygon. The sum of the interior angles of a quadrilateral is 360°

When we divide the quadrilateral into two triangles, each triangle has an angle sum of 180 degree, so the sum of angles in a quadrilateral is 360.

Find the value of x in the following quadrilaterals :

Problem 1 :

Solution :

Sum of interior angles of a quadrilateral = 360

x + 110 + 105 + 80 = 360

x + 295 = 360

Subtracting 295 on both sides.

x = 360 - 295

x = 65

Problem 2 :

Solution :

x + 56 + 121 + 90 = 360

x + 267 = 360

Subtracting 267 on both sides.

x = 360 - 267

x = 93

Problem 3 :

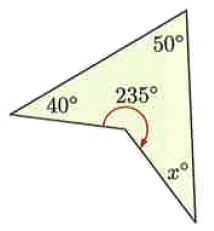
Solution :

40 + 235 + x + 50 = 360

325 + x = 360

Subtracting 325 on both sides.

x = 360 - 325

x = 35

Problem 4 :

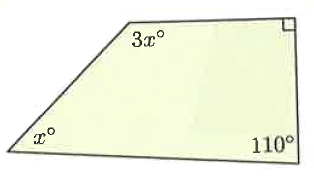
Solution :

x + 3x + 110 + 90 = 360

4x + 200 = 360

Subtracting 200 on both sides.

4x = 360 - 200

4x = 160

Dividing by 4 on both sides.

x = 160/4

x = 40

Problem 5 :

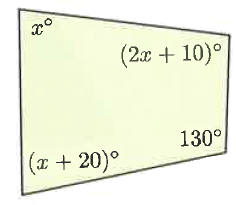
Solution :

x + 20 + 130 + 2x + 10 + x = 360

4x + 160 = 360

Subtracting 160 on both sides.

4x = 360 - 160

4x = 200

Dividing by 4 on both sides.

x = 200/4

x = 50

Problem 6 :

Find the values of a and b.

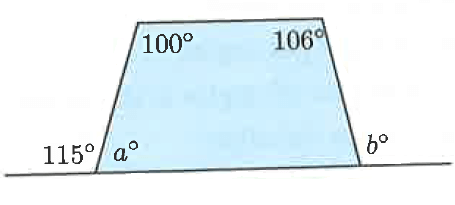
Solution :

115 + a = 180

Subtracting 115 on both sides.

a = 180 - 115

a = 65

Sum of interior angles of a quadrilateral = 360

a + 100 + 106 + b = 360

65 + 100 + 106 + b = 360

271 + b = 360

Subtracting 271 on both sides.

b = 360 - 271

b = 89

Problem 7 :

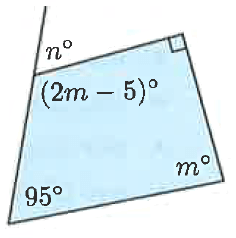
Solution :

Sum of interior angles of a quadrilateral = 360

m + 95 + 2m - 5 + 90 = 360

3m + 90 + 90 = 360

3m + 180 = 360

Subtracting 180 on both sides.

3m = 360 - 180

3m = 180

Dividing by 3 on both sides.

m = 180/3

m = 60

2m - 5 and n are linear pair.

2m - 5 + n = 180

2(60) - 5 + n = 180

120 - 5 + n = 180

115 + n = 180

Subtracting 115 on both sides.

n = 180 - 115

n = 65

Problem 8 :

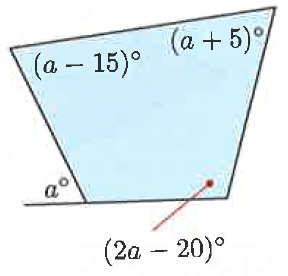
Solution :

a - 15 + a + 5 + 2a - 20 + 180 - a = 360

3a - 15 - 20 + 5 + 180 = 360

3a + 150 = 360

Subtracting 150 on both sides.

3a = 360 - 150

3a = 210

Dividing by 3 on both sides.

a = 210/3

a = 70