INEQUALITIES INVOLVING QUADRATIC TERMS

Inequalities involving x² rather than x can still be solved. For example, the inequality

x² < 9

will be satisfied by any number between − 3 and 3. So the solution is written as

−3 < x < 3

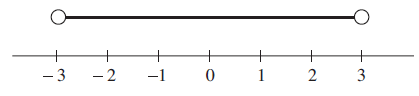
The end points of the intervals are defined as √9 = ± 3.

If the inequality had been x² > 9, then it would be satisfied if x was greater than 3 or if x was less than − 3. So the solution will be

x > 3 or x < − 3

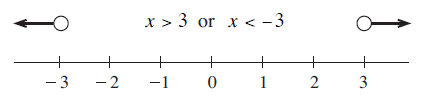
Note :

For this type of inequality it is very easy to find the end points but care must be taken when deciding whether it is the region between the points or the region outside the points which is required.

Testing a point in a region will confirm whether your answer is correct.

For example,

for x² > 9, test x = 2, which gives 4 > 9. This is not true, so the region between the points is the wrong region; the region outside the points is needed.

Show on a number line the solutions to :

Problem 1 :

x² ≥ 16

Solution :

The solution to x² ≥ 16 is

x ≥ √16

x ≤ -4 or x ≥ 4

Which is shown below.

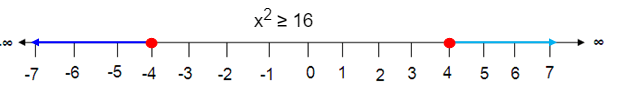
Problem 2 :

x² < 25

Solution :

The solution of x² < 25 is

x < √25

-5 < x < 5

Which is shown below.

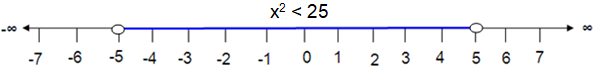
Illustrate the solutions  to the following inequalities on a number line.

Problem 3 :

x² < 1

Solution :

The solution of x² < 1 is

x < √1

x < ±1

-1 < x < 1

Which is shown below.

Problem 4 :

x² ≥ 4

Solution :

The solution to x² ≥ 4 is

x ≥ √4

x ≤ -2 or x ≥ 2

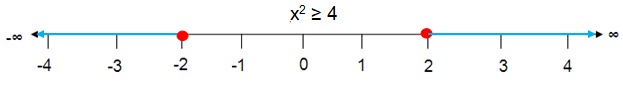
Problem 5 :

x² ≥ 25

Solution :

The solution to x² ≥ 25 is

x ≥ √25

x ≤ -5 or x ≥ 5

Which is shown below.

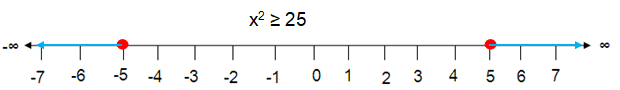
Problem 6 :

x² < 49

Solution :

The solution of x² < 49 is

x < √49

-7 < x < 7

Which is shown below.

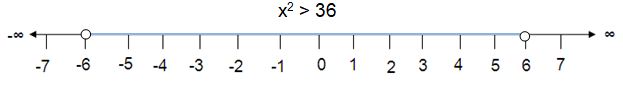
Problem 7 :

x² > 4

Solution :

The solution of x² > 4 is

x > √4

-2 < x < 2

Which is shown below.

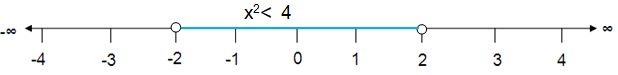
Problem 8 :

x² ≥ 6.25

Solution :

The solution to x² ≥ 6.25 is

x ≥ √6.25

x ≤ -2.5 or x ≥ 2.5

Which is shown below.

Problem 9 :

x² < 0.25

Solution :

The solution of x² < 0.25 is

x > √0.25

-0.5 < x < 0.5

Which is shown below.

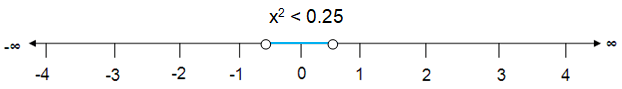
Problem 10 :

x² ≥ 2.25

Solution :

The solution to x² ≥ 2.25 is

x ≥ √2.25

x ≥ 1.5

x ≤ -1.5 or x ≥ 1.5

Which is shown below.