INCREASING AND DECREASING INTERVALS ON A GRAPH

Always, we have to observe the graph from left to right.

Increasing function :

When we observe the graph from left to right, if it raises or goes up, we should call it as increasing function.

Finding increasing interval :

A function is increasing on an interval if, for any x₁ and x₂ in the interval, x₁ < x₂ implies f(x₁) < f(x₂)

Decreasing function :

When we observe the graph from left to right, if it falls or goes down, we should call it as decreasing function.

Finding decreasing interval :

A function is decreasing on an interval if, for any x₁ and x₂ in the interval, x₁ < x₂ implies f(x₁) > f(x₂)

Constant function :

When we observe the graph, if there is no change, we should call it as constant function.

A function is constant on an interval if, for any x₁ and x₂ in the interval, f(x₁) = f(x₂)

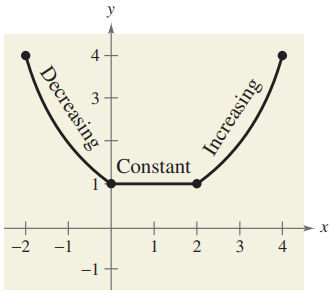
• Decreasing interval is (-2, 0)
• Constant is at (0, 2)
• Increasing is at (2, 4)

Problem 1 :

Use the graph given below to describe increasing, or decreasing behavior of each function.

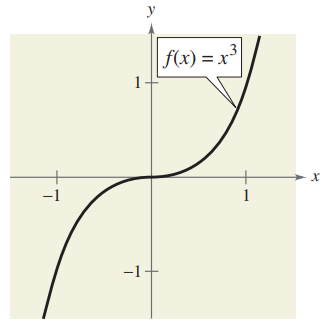
Solution :

By observing the graph from left to right, it is going up only. The function is increasing for all real numbers,

Problem 2 :

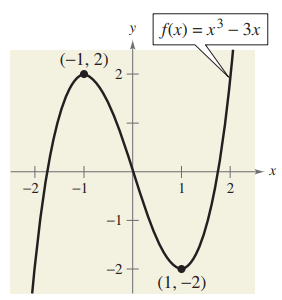
Solution :

• At (-∞, -1) and (1, ∞) it is increasing.
• At (-1, 1), it is decreasing.

Problem 3 :

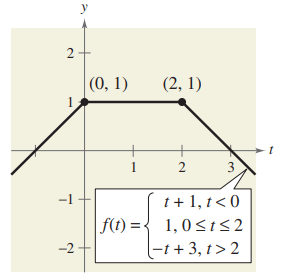
Solution :

• At (-∞, 0) it is increasing.
• At (0, 2), it is constant function.
• At (2, ∞), it is decreasing function.

Problem 4 :

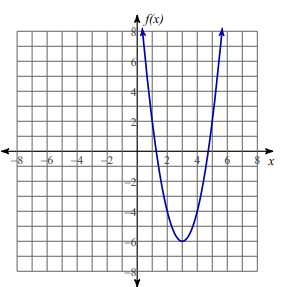
Solution :

By observing the graph above, 

• Decreasing at (-∞, 3)
• Increasing at (3, ∞)

Problem 5 :

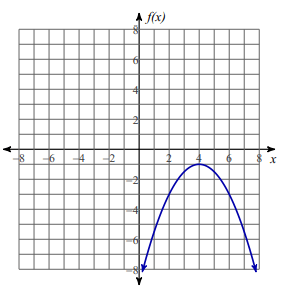
Solution :

By observing the graph above, 

• Decreasing at (4, ∞)
• Increasing at (-∞, 4)

Problem 6 :

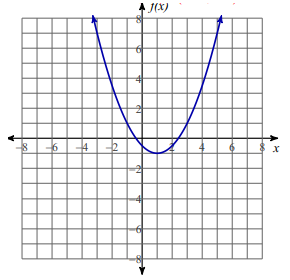
Solution :

By observing the graph above, 

• Decreasing at (-∞, 1)
• Increasing at (1, ∞)

Problem 7 :

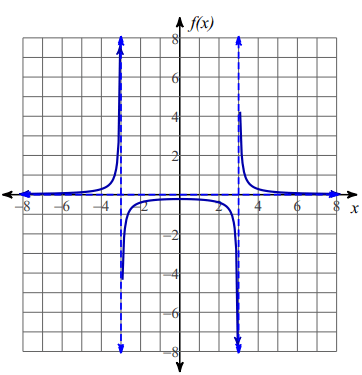
Solution :

By observing the graph above, 

• Increasing at (-∞, -3) and (-3, 0)
• Decreasing at (0, 3) and (3, ∞)

At x = -3 and x = 3, we have vertical asymptotes.