IDENTIFYING TRANSFORMATIONS OF QUADRATIC FUNCTIONS

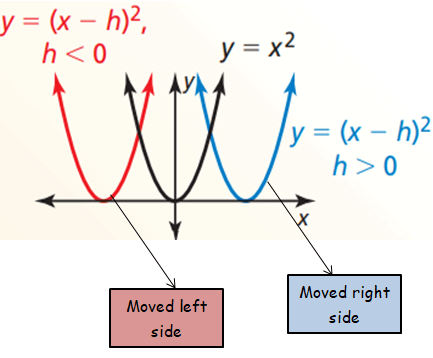
Translation

f(x) = a(x − h)² + k

Horizontal translation :

Moving the graph towards left or right.

h > 0, then move the graph right.

h < 0, then move the graph left.

Vertical translation :

Moving the graph towards up or down.

k > 0, then move the graph up.

k < 0, then move the graph down.

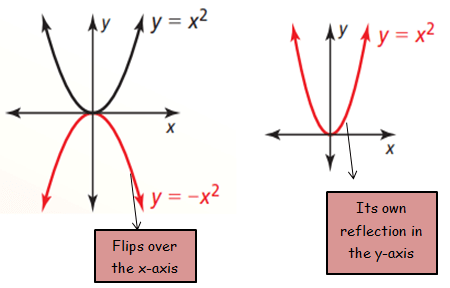
Reflection

Reflection across x-axis :

f(x) = x²

-f(x) = -x²

Reflection across y-axis :

f(x) = x²

f(-x) = (-x)²

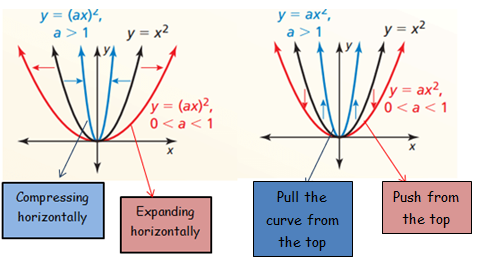
Shrinks and Stretches

Horizontal stretches and shrinks :

f(x) = x²

f(ax) = (ax)²

If a > 1 (horizontal shrink)

If 0 < a < 1 (horizontal stretch)

Vertical stretches and shrinks :

f(x) = x²

a f(x) = ax²

If a > 1 (vertical stretch)

If 0 < a < 1 (vertical shrink)

Problem 1 :

Which correctly identifies the values of the parameters a, h, and k for the function

𝑓(𝑥) = −(𝑥 − 1)² − 4

a.𝑎 = 1, ℎ = −1, 𝑘 = −4            b. 𝑎 = −1, ℎ = 1, 𝑘 = −4

c. 𝑎 = −1, ℎ = −1, 𝑘 = −4      d. 𝑎 = −1, ℎ = 1, 𝑘 = 4

Solution :

𝑓(𝑥) = −(𝑥 − 1)² − 4

By comparing the given function with general form of quadratic function with vertex (h, k), we get

f(x) = a(x - h)² + k

Here a = -1, h = 1 and k = -4

Problem 2 :

What is the equation of this graph?

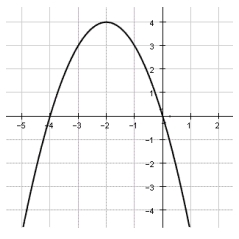
a. y = x² - 4x       b.  -x² - 4x       c. -x² - 4      d. -x² + 4

Solution :

Quadratic function in vertex form will be 

f(x) = a(x - h)² + k

By observing the figure, vertex is (-2, 4) and it passes through the point (0, 0).

h = -2 and k = 4

f(x) = a(x - (-2))² + 4

f(x) = a(x + 2)² + 4

It passes through (0, 0).

0 = a(0 + 2)² + 4

4a = -4

a = -1

Applying the value, we get

f(x) = -1(x + 2)² + 4

Expanding it, we get

f(x) = -1(x² + 4x + 4) + 4

f(x) = -1x² - 4x - 4 + 4

f(x) = -1x² - 4x

Problem 3 :

Which function includes a translation of 2 two units to the right?

a. 𝑓(𝑥) = 𝑥² + 2                  b. 𝑓(𝑥) = (𝑥 − 2)² − 3

c. 𝑓(𝑥) = (𝑥 + 2)² − 4         d. 𝑓(𝑥) = 2𝑥²

Solution :

Option a :

𝑓(𝑥) = 𝑥² + 2

K = 2, vertically moving the graph two units up.

Option b :

𝑓(𝑥) = (𝑥 − 2)² − 3

here h = 2 and k = -3

so, move the graph horizontally 2 units right and move vertically 3 units. down. then option b is correct.

Problem 4 :

Which function includes a translation of 4 units to the left and a vertical compression to the graph of 𝑓(𝑥) = 𝑥² ?

a. 𝑓(𝑥) = 1/3(𝑥 - 4)²                  b. 𝑓(𝑥) = 3(𝑥 − 4)²

c. 𝑓(𝑥) = 1/3(𝑥 + 4)²                  b. 𝑓(𝑥) = 3(𝑥 + 4)²

Solution :

𝑓(𝑥) = 𝑥²

Here h = -4 and the value of a should lie between 0 to 1 since it is vertical compression.

In 𝑓(𝑥) = 1/3(𝑥 + 4)² 

h = -4 and a = 1/3 (0 < a < 1)

So, option c is correct.

Problem 5 :

List the sequence of steps required to graph the function

𝑦 = −(𝑥 − 3)² − 2

a. horizontal translation 3 units to the right, vertical compression by a factor of 1, vertical translation 2 units down

b. horizontal translation 3 units to the right, reflection in x-axis, vertical translation 2 units down.

c. horizontal translation 3 units to the left, vertical translation 2 units up, reflection in x-axis.

d. horizontal translation 3 units to the left, reflection in x-axis, vertical translation 2 units down

Solution :

𝑦 = −(𝑥 − 3)² − 2

Reflection across x-axis, h = 3 and k = -2

After reflection across x-axis, the graph is moved 3 units right and 2 units down. So, option b is correct.

Problem 6 :

Which function matches the graph?

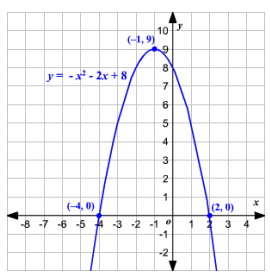
a. 𝑓(𝑥) = (𝑥 + 1)² + 9       b. 𝑓(𝑥) = (𝑥 − 1)² + 9

c. 𝑓(𝑥) = −(𝑥 + 1)² + 9       d. 𝑓(𝑥) = −(𝑥 − 1)² + 9

Solution :

The given graph is opening down, so reflection across x-axis is made. h = -1 and k = 9. So, option c is the answer.

Problem 7 :

Match the description to its equations. Vertical stretch by a factor of 5.

a. 𝑓(𝑥) = 5𝑥²                   b. 𝑓(𝑥) = (5𝑥)²

c. 𝑓(𝑥) = 1/5 (𝑥)²            d. 𝑓(𝑥) = ( 1/5 𝑥)²

Solution :

Vertical stretch means, the value of a would be greater than 1. So, the answer will be option a.

Problem 8 :

If 0 < 𝑎 < 1, what would be the transformation of, 𝑎 , from the quadratic parent function, 𝑓(𝑥) = 𝑥² ?

a. 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑠𝑡𝑟𝑒𝑡𝑐ℎ

b. 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑐𝑜𝑚𝑝𝑟𝑒𝑠𝑠𝑖𝑜𝑛

c. ℎ𝑜𝑟𝑖𝑧𝑎𝑛𝑡𝑎𝑙 𝑠ℎ𝑖𝑓𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑟𝑖𝑔ℎ𝑡

d. ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙 𝑠ℎ𝑖𝑓𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑙𝑒𝑓𝑡

e. 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑠ℎ𝑖𝑓𝑡 𝑢𝑝

f. vertical shift down

Solution :

Since the value of a lies between 0 to 1, vertical compression can be done. So, the answer is option b.

Problem 9 :

If ℎ > 0 what would be the transformation of, ℎ , in the vertex form of the quadratic equation 𝑦 = 𝑎(𝑥 − ℎ) ² + 𝑘?

a. 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑠𝑡𝑟𝑒𝑡𝑐ℎ

b. 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑐𝑜𝑚𝑝𝑟𝑒𝑠𝑠𝑖𝑜𝑛

c. ℎ𝑜𝑟𝑖𝑧𝑎𝑛𝑡𝑎𝑙 𝑠ℎ𝑖𝑓𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑟𝑖𝑔ℎ𝑡

d. ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙 𝑠ℎ𝑖𝑓𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑙𝑒𝑓𝑡

e. 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑠ℎ𝑖𝑓𝑡 𝑢𝑝

f. vertical shift down

Solution :

Horizontal shift to the right.