IDENTIFYING THE CHARACTERISTICS OF EXPONENTIAL FUNCTIONS

Identifying exponential growth and decay from graph

While observing the graph from left to right,

• If it is goes up, then it must be exponential growth function.
• If it is goes down, then it must be exponential decay function.

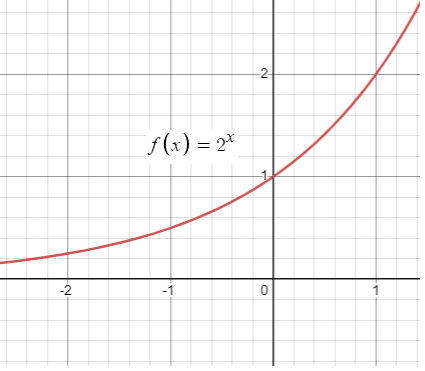
In other words, it is known as increasing function. Concave up.

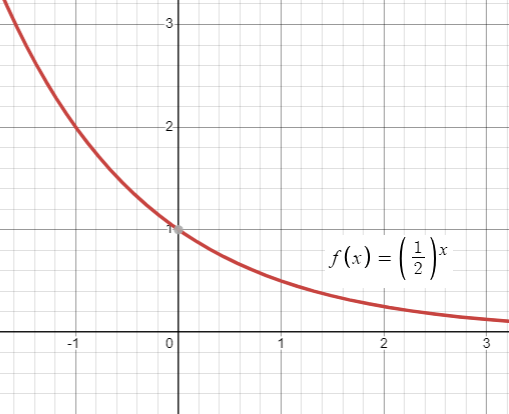
In other words, it is known as decreasing function. Concave down.

Answer the questions for each exponential function.

Problem 1 :

f(x) = 7(2^x)

a) Is the function increasing or decreasing 

b) Is the function concave up or down

c)  Find lim x->-∞ f (x)

d)  Find lim x->∞ f (x)

Solution :

f(x) = 7(2^x)

Here a = 7 and b = 2 > 1, it must be exponential growth function.

a) Since it is exponential growth function, it is increasing function.

b)  Concave up

c)  Horizontal asymptote is y = 0 or x-axis.

Domain is (-∞, ∞) and range is (0, ∞)

lim x->-∞ f (x) = 0

d)  lim x->∞ f (x) = ∞

Problem 2 :

f(x) = -4(5^x)

a) Is the function increasing or decreasing 

b) Is the function concave up or down

c)  Find lim x->-∞ f (x)

d)  Find lim x->∞ f (x)

Solution :

f(x) = -4(5^x)

Here a = 4 and b = 5 > 1, it must be exponential growth function. Since we have negative coefficient, it must be reflection about x-axis.

a) It is decreasing function.

b)  Concave down

c)  Horizontal asymptote is y = 0 or x-axis.

Domain is (-∞, ∞) and range is (0, -∞)

lim x->-∞ f (x) = 0

d)  lim x->∞ f (x) = -∞

Problem 3 :

f(x) = (0.2^x)

a) Is the function increasing or decreasing 

b) Is the function concave up or down

c)  Find lim x->-∞ f (x)

d)  Find lim x->∞ f (x)

Solution :

f(x) = (0.2)^x

Here a = 1 and b = 0.2 in between 0 to 1, it must be exponential decay function. 

a) It is decreasing function.

b)  Concave up

c)  Horizontal asymptote is y = 0 or x-axis.

Domain is (-∞, ∞) and range is (0, ∞)

lim x->-∞ f (x) = ∞

d)  lim x->∞ f (x) = 0

Problem 4 :

f(x) = -6(0.8^x)

a) Is the function increasing or decreasing 

b) Is the function concave up or down

c)  Find lim x->-∞ f (x)

d)  Find lim x->∞ f (x)

Solution :

f(x) = -6(0.8^x)

Here a = 6 and b = 0.8 in between 0 to 1, it must be exponential decay function. Since we have negative coefficient, it must be the reflection across x-axis.

a) It is decreasing function.

b)  Concave down

c)  Horizontal asymptote is y = 0 or x-axis.

Domain is (-∞, ∞) and range is (0, -∞)

lim x->-∞ f (x) = 0

d)  lim x->∞ f (x) = -∞

Problem 5 :

f(x) = 6(1/9)^x

a) Is the function increasing or decreasing 

b) Is the function concave up or down

c)  Find lim x->-∞ f (x)

d)  Find lim x->∞ f (x)

Solution :

f(x) = 6(1/9)^x

Here a = 6 and b = 1/9 in between 0 to 1, it must be exponential decay function. 

a) It is decreasing function.

b)  Concave up

c)  Horizontal asymptote is y = 0 or x-axis.

Domain is (-∞, ∞) and range is (0, ∞)

lim x->-∞ f (x) = ∞

d)  lim x->∞ f (x) = 0

Problem 6 :

f(x) = -(0.4)^x

a) Is the function increasing or decreasing 

b) Is the function concave up or down

c)  Find lim x->-∞ f (x)

d)  Find lim x->∞ f (x)

Solution :

f(x) = -(0.4)^x

Here a = 1 and b = 0.4 in between 0 to 1, it must be exponential decay function. Since we have negative coefficient, it must be the reflection across x-axis.

a) It is increasing  function.

b)  Concave down

c)  Horizontal asymptote is y = 0 or x-axis.

Domain is (-∞, ∞) and range is (0, -∞)

lim x->-∞ f (x) = -∞

d)  lim x->∞ f (x) = 0

Problem 7 :

The exponential function 𝑓 is defined by f(X) = ab^x, where a and b are positive integers.

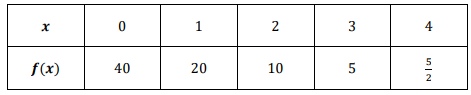
Which of the following statement is true ?

(A) 𝑓 demonstrates exponential decay because 𝑎 > 0 and 0 <𝑏< 1.

(B) 𝑓 demonstrates exponential decay because 𝑎 > 0 and 𝑏 > 1.

(C) 𝑓 demonstrates exponential growth because 𝑎 > 0 and 0 < 𝑏 < 1.

(D) 𝑓 demonstrates exponential growth because 𝑎 > 0 and 𝑏 > 1.

Solution :

Every exponential function will be in the form f(X) = ab^x

From the table, applying the points (0, 40) and (1, 20), we get

f(0) = ab⁰

40 = a(1)

a = 40

Then f(x) = 40 b^x

Applying (1, 20), we get

20 = 40(b)¹

b = 1/2

a > 1 and b lies in between 0 and 1.

Exponential decay and option A is correct.