IDENTIFYING EACH RELATION AS DIRECT PARTIAL OR INVERSE VARIATION

Identify each relation as direct variation, a partial variation or neither.

Problem 1 :

y = 3x

Solution :

The given function is in the form, y = kx. So it is direct variation.

Problem 2 :

y = 2x + 1

Solution :

The given function is in the form, y = mx + b. So it is in partial variation.

Problem 3 :

a)  Compete the table of values given that y varies partially with x.

b) Identify the initial value of y and the constant of variation from the table.

c) Write the equation relating y and x in the form y = mx + b.

Solution :

Since the given table represents partial variation, it will satisfy in the form y = mx + b

Applying x = 0 and y = 5

5 = m(0) + b

b = 5

Applying the value of b, we get

y = mx + 5

Applying x = 3 and y = 20

20 = m(3) + 5

3m = 20 - 5

3m = 15

m = 15/3

m = 5

Applying the value of m, we get

y = 5x + 5

When y = 40, x = ?

40 = 5x + 5

40 - 5 = 5x

5x = 35

x = 35/5

x = 7

b) Here the constant of variation is the value of m, it is 5.

c) y = 5x + 5

Problem 4 :

A small pizza costs $7 plus $1.50 per topping.

a) Identify the fixed cost and variable cost of this partial variation.

b) Determine the equation relating the cost C and the number of topping n.

c) Use the equation to determine the cost of a small pizza with five toppings.

Solution :

Cost of pizza = C and number of toppings = n

C = 7 + 1.50 n

a) fixed cost = 7, variable cost = 1.50

b) C = 7 + 1.50 n

c)  When number of toppings = 5

C = 7 + 1.50(5)

= 7 + 7.5

= 14.5

Cost of pizza with 5 topping is $14.5.

Problem 5 :

A class is planning a field trip to an art gallery. The cost of renting bus is $250. There is an additional cost of $4 per student for the entrance fee.

a) Identify the fixed cost and the variable cost of this partial variation.

b) Write and equation relating cost C, in dollars, the number of students n.

c) Use the equation to determine the total cost if 25 students attend.

Solution :

a) Cost of renting bus = fixed cost = 250

Entrance fee per student = 4 = variable cost

b) C = 250 + 4n

c) When n = 25

C = 250 + 4(25)

= 250 + 100

= 350

Problem 6 :

The table shows the amount of printing company charges for advertising figures.

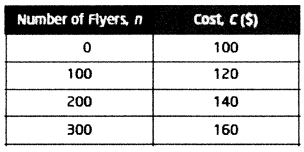
a) Identify the fixed cost this company charges for pictures the flyers.

b) Determine the variable cost of producing one flyer. 

c) Write the equation representing the price of flyers.

d) How many flyers can be produced for $280 ?

Solution :

When producing 0 flyers, the company charges 100

a) Fixed cost (b) = 100

Let m be variable cost 

C = nx + b

b)  When n = 0, b = 100

100 = n(0) + b

100 = b

C = nx + 100

Applying n = 100, C = 120

120 = 100x + 100

120 - 100 = 100x 

20 = 100x 

x = 20/100

x = 1/5 ==> 0.2

y = 0.2n + 100

c)  y = 0.2x + 100

d) When C = 280

280 = 0.2n + 100

280 - 100 = 0.2n

180 = 0.2n

180/0.2 = n

n = 900

So, 900 flyers can be produced.

Problem 7 :

A computer decreases in value over time. The relationship between the value of the computer, v, in dollars after t years is written as the equation v = -300t + 2100. A line representing the relationship is graphed. What does the vintercept of the line represent?

a) The decrease in value per year

b) The initial value of the computer

c) The number of years until the value is $0

d) The number of years the computer will work

Solution :

The initial value of the computer