IDENTIFY CHARACTERISTICS OF QUADRATIC FUNCTIONS

Graph each quadratic equation and identify all the following information

Problem 1 :

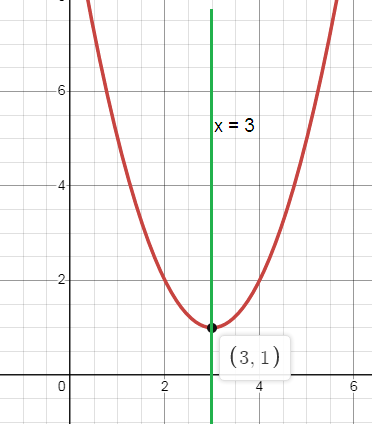
f(x) = (x - 3)² + 1

Solution:

a. Since the value of a is positive, it will open up.

Opens Up 

b. Axis of symmetry:

x = 3

c. Vertex:

(h, k) = (3, 1)

d. Since the parabola opens up, it will have minimum.

e. y-intercept:

x = 0

y = (0 - 3)² + 1

y = 9 + 1

y = 10

(0, 10)

f. Domain:         

All real numbers

Range:

y ≥ 1

g. Roots:

x-intercepts are roots.

Ø

Problem 2 :

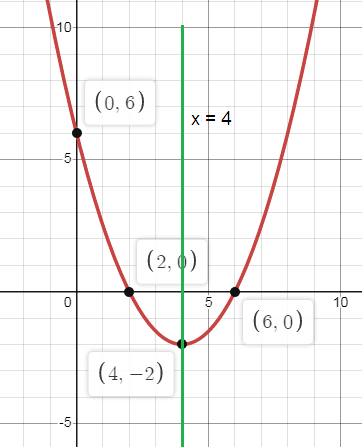
f(x) = 1/2(x - 4)² - 2

Solution:

a. Circle one:

Opens Up 

b. Axis of symmetry:

x = 4

c. Vertex:

(h, k) = (4, -2)

d. Circle one:

Minimum 

e. y-intercept:

x = 0

y = 1/2(0 - 4)² - 2

y = 8 - 2

y = 6

(0, 6)

f. Domain:         

All real numbers

Range:

y ≥ -2

g. Roots:

X = {2, 6}

Problem 3 :

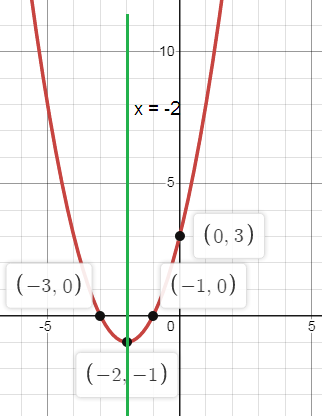
f(x) = (x + 2)² - 1

Solution:

a. Circle one:

Opens Up 

b. Axis of symmetry:

x = -2

c. Vertex:

(h, k) = (-2, -1)

d. Circle one:

Minimum 

e. y-intercept:

x = 0

y = (0 + 2)² - 1

y = 4 - 1

y = 3

(0, 3)

f. Domain:         

All real numbers

Range:

y ≥ -1

g. Roots:

X = {-3, -1}

Problem 4 :

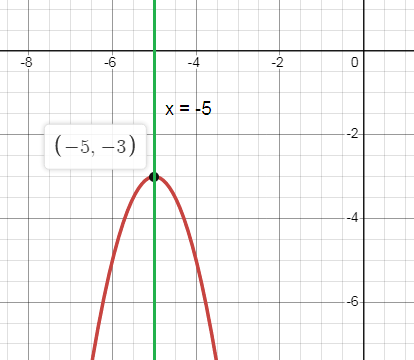
f(x) = -2(x + 5)² - 3

Solution:

a. Circle one:

Opens Down 

b. Axis of symmetry:

x = -5

c. Vertex:

(h, k) = (-5, -3)

d. Circle one:

Maximum 

e. y-intercept:

x = 0

y = -2(0 + 5)2 - 3

y = -2(25) - 3

y = -50 - 3

y = -53

(0, -53)

f. Domain:         

All real numbers

Range:

y ≤ -3

g. Roots:

Ø

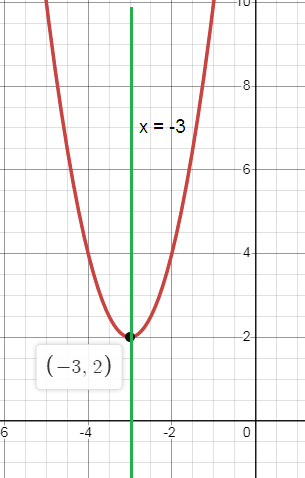
Problem 5 :

f(x) = 2(x + 3)² + 2

Solution:

a. Circle one:

Opens Up

b. Axis of symmetry:

x = -3

c. Vertex:

(h, k) = (-3, 2)

d. Circle one:

Minimum 

e. y-intercept:

x = 0

y = 2(0 + 3)² + 2

y = 2(9) + 2

y = 18 + 2

y = 20

(0, 20)

f. Domain:         

All real numbers

Range:

y ≥ -3

g. Roots:

Ø

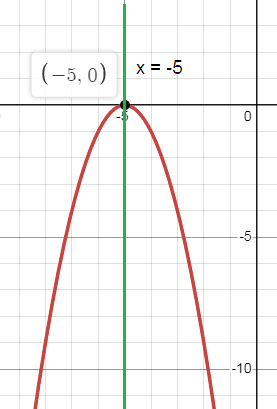
Problem 6 :

f(x) = -(x + 5)²

Solution:

a. Circle one:

Opens Down

b. Axis of symmetry:

x = -5

c. Vertex:

(h, k) = (-5, 0)

d. Circle one:

Maximum 

e. y-intercept:

x = 0

y = -(0 + 5)² 

y = -25

(0, -25)

f. Domain:         

All real numbers

Range:

y ≤ 0

g. Roots:

X = {-5}

Problem 7 :

The height of a ball that is thrown is given by the equation h = -5(t - 3)² + 46.5 gives the height of the half t seconds after it is thrown.

a. Write the equation of the axis of symmetry and find the coordinates of the vertex.

b. Graph the function.

c. What is the maximum height that ball reaches?

d. How many seconds is the ball in the air?

e. What is the domain and range of the ball?

f. What was the height of the ball after 1 second?

Solution:

a.

y = a(x - h)² + k

h = -5(t - 3)² + 46.5

vertex (h, k) = (3, 46.5)

Axis of symmetry x = h

x = 3

b.

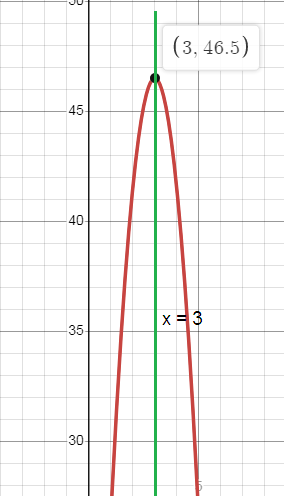
c.

Maximum height = 46.5 meters

d.

3 seconds

e.

Domain:

0 ≤ x ≤ 3

Range:

0 ≤ y ≤ 46.5

f.

h = -5(1 - 3)² + 46.5

h = -5(4) + 46.5

h = -20 + 46.5

h = 26.5 meters

Problem 8 :

A football is kicked into the air. Its height in meters after t seconds is given by

h = -4.9(t - 2.4)² + 29

a. What was the height of the football when it was kicked?

b. What was the maximum height of the ball?

c. Graph the function.

d. How high was the ball after 2 seconds?

e. Was the ball still in the air after 5 seconds?

Solution:

a.

h = -4.9(0 - 2.4)² + 29

= -4.9(-2.4)² + 29

= -4.9(5.76) + 29

= -28.224 + 29

h = 0.776 meters

b.

Maximum height = 29 meters

c.

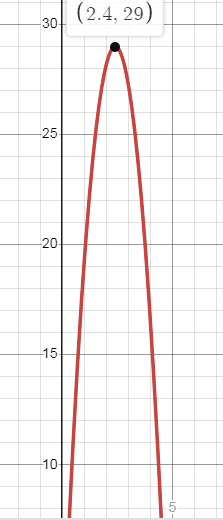
d.

t = 2

y = -4,9(2 - 2.4)2 + 29

= -4.9(-0.4)2 + 29

= -4.9(0.16) + 29

= -0.784 + 29

y = 28.22 meters

e.

t = 5

y = -4.9(5 - 2.4)2 + 29

y = -4.9(2.6)2 + 29

= -4.9(6.76) + 29

= -33.124 + 29

y = -4.124

After 5 seconds ball will not be in the air.