IDENTIFYING CHARACTERISTICS OF QUADRATIC FUNCTIONS WORKSHEET

Graph each quadratic equation and identify all the following information

a. Opens Up or Down

b. Axis of symmetry:

c: Vertex:

d. Minimum or Maximum

e. y-intercept:

f. Domain:           Range:

g. Roots:

Problem 1 :

f(x) = (x - 3)2 + 1 

Solution

Problem 2 :

f(x) = 1/2(x - 4)2 - 2

Solution

Problem 3 :

f(x) = (x + 2)2 - 1

Solution

Problem 4 :

f(x) = -2(x + 5)2 - 3

Solution

Problem 5 :

f(x) = 2(x + 3)2 + 2

Solution

Problem 6 :

f(x) = -(x + 5)2

Solution

Problem 7 :

The height of a ball that is thrown is given by the equation h = -5(t - 3)2 + 46.5 gives the height of the half t seconds after it is thrown.

a. Write the equation of the axis of symmetry and find the coordinates of the vertex.

b. Graph the function.

c. What is the maximum height that ball reaches?

d. How many seconds is the ball in the air?

e. What is the domain and range of the ball?

f. What was the height of the ball after 1 second?

identify-char-of-quad-fun-q7.png

Solution

Problem 8 :

A football is kicked into the air. Its height in meters after t seconds is given by

h = -4.9(t - 2.4)2 + 29

a. What was the height of the football when it was kicked?

b. What was the maximum height of the ball?

c. Graph the function.

d. How high was the ball after 2 seconds?

e. Was the ball still in the air after 5 seconds?

Solution

Answer Key

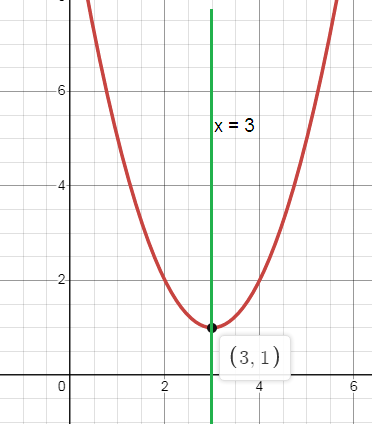
1)  Opens Up 

b. Axis of symmetry: x = 3

c. Vertex: (h, k) = (3, 1)

d. minimum.

e. y-intercept:(0, 10)

f. Domain: All real numbers

Range: y ≥ 1

g. Roots: No x-intercept that is no roots.

identify-char-of-quad-fun-q1

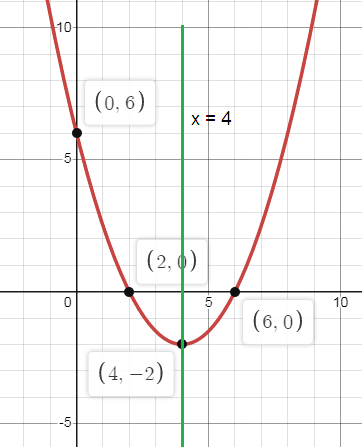
2)  Opens Up 

b. Axis of symmetry: x = 4

c. Vertex: (h, k) = (4, -2)

d. Minimum 

e. y-intercept: (0, 6)

f. Domain: All real numbers

Range: y ≥ -2

g. Roots: x = {2, 6}

identify-char-of-quad-fun-q2.png

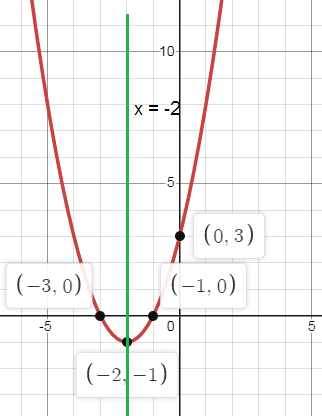
3)  Opens Up 

b. Axis of symmetry: x = -2

c. Vertex: (h, k) = (-2, -1)

d. Minimum 

e. y-intercept: (0, 3)

f. Domain: All real numbers

Range: y ≥ -1

g. Roots: x = {-3, -1}

identify-char-of-quad-fun-q3.png

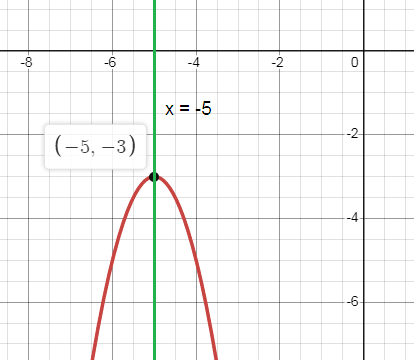
4)  Opens Down 

b. Axis of symmetry: x = -5

c. Vertex: (h, k) = (-5, -3)

d. Maximum 

e. y-intercept: (0, -53)

f. Domain:  All real numbers

Range: y ≤ -3

g. Roots: No x-intercept

identify-char-of-quad-fun-q4.png

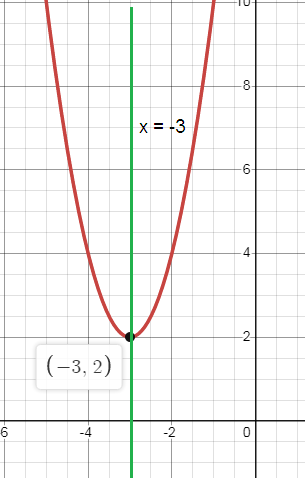
5) Opens Up

b. Axis of symmetry: x = -3

c. Vertex: (h, k) = (-3, 2)

d. Minimum 

e. y-intercept:  (0, 20)

f. Domain:  All real numbers

Range: y ≥ -3

g. Roots:  No x0intercept

identify-char-of-quad-fun-q5.png

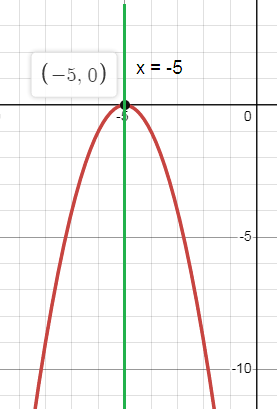
6)  Opens Down

b. Axis of symmetry: x = -5

c. Vertex: (h, k) = (-5, 0)

d. Maximum 

e. y-intercept: (0, -25)

f. Domain: All real numbers

Range: y ≤ 0

g. Roots x = {-5}

identify-char-of-quad-fun-q6.png

7) a.

y = a(x - h)2 + k

h = -5(t - 3)2 + 46.5

vertex (h, k) = (3, 46.5)

Axis of symmetry x = h

x = 3

b.

identify-char-of-quad-fun-s7.png

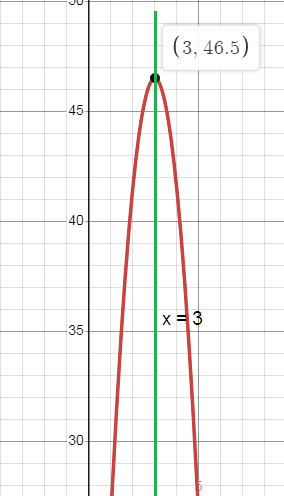
c. Maximum height = 46.5 meters

d. 3 seconds

e. Domain: 0 ≤ x ≤ 3

Range: 0 ≤ y ≤ 46.5

f. h = 26.5 meters

8)  a. h = 0.776 meters

b. Maximum height = 29 meters

c.

identify-char-of-quad-fun-s8.png

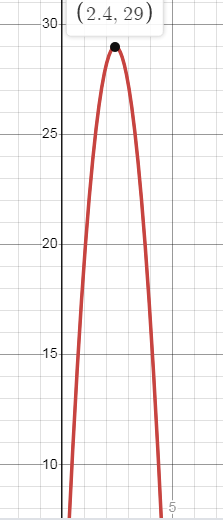
d. y = 28.22 meters

e. After 5 seconds ball will not be in the air.

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More