IDENTIFY THE PARENT FUNCTION AND THE TRANSFORMATION SHOWN IN THE FUNCTIONS

Linear function :

The parent function of any linear function will be in the form,

y = mx + b

The graphical form of the linear function is a straight line.

Quadratic function :

The parent function of any quadratic function will be in the form,

y = a(x - h)² + k

The graphical form a quadratic function is a parabola.

Absolute value function :

The parent function of any absolute value function will be

y = a|x - h| + k

Its graphical form will be the shape of V.

Exponential function :

The parent function of any exponential function will be

y = ab^{(x - h)} + k

identify the function family to which f belongs. Compare the graph of f to the graph of its parent function.

Problem 1 :

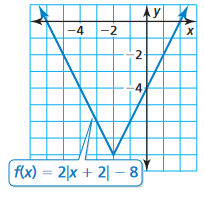
Solution :

The given graph is the graph of absolute value function.

Parent function :

y = |x|

Equation of given function :

f(x) = 2|x + 2| - 8

Transformations done :

Vertical stretch of 2 units, horizontal translation of 2 units left and vertical translation of 8 units down.

Problem 2 :

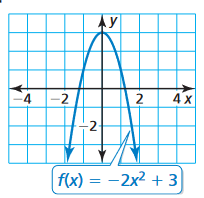
Solution :

The given graph is the graph of quadratic function.

Parent function :

y = x²

Equation of given function :

f(x) = -2 x² + 3

Transformations done :

Vertical stretch of 2 units, reflection over the x-axis. No horizontal translation and vertical translation of 8 units down.

Problem 3 :

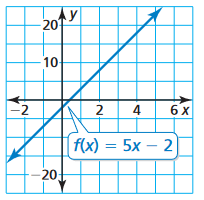
Solution :

The given graph is the graph of linear function.

Parent function :

y = mx + b

Equation of given function :

f(x) = 5 x - 2

Transformations done :

Vertical stretch of 5 units, and vertical translation of 2 units down.

Graph the function and its parent function. Then describe the transformation

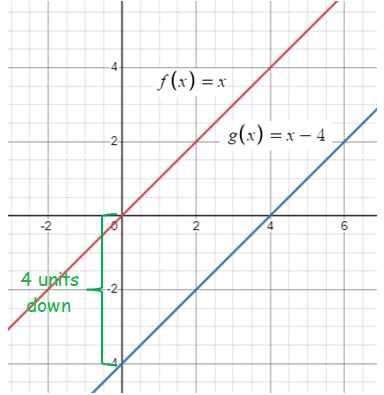
Problem 4 :

g(x) = x - 4

Solution :

The function g is a linear function. Parent function of linear function is y = x.

By comparing the given function g(x) with parent function, we know that it the parent function should be moved 4 units down.

Points from the parent function :

(0, 0) (1, 1) (2, 2) (4, 0)

Points from the function after transformation :

(0, -4) (1, -3) (2, -2) and (4, 0).

Write the equation for the following translations of their particular parent graphs. You may use y = or function notation (the f(x) type notation).

Problem 5 :

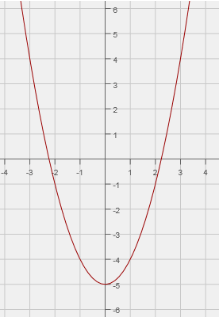
Solution :

The given graph is in the form of u, so it must be a quadratic function.

f(x) = x²

Moving the graph 5 units down.

So, the required function will be 

f(x) = x² - 5

Problem 6 :

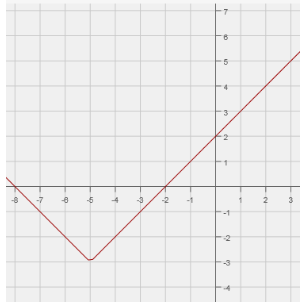
Solution :

The given graph is in the form of V, so it must be a absolute value function.

f(x) = |x|

Moving the graph 3 units down and 5 units left.

f(x) = |x - (-5)| - 3

f(x) = |x + 5| - 3

So, the required function will be 

f(x) = |x + 5| - 3

Problem 7 :

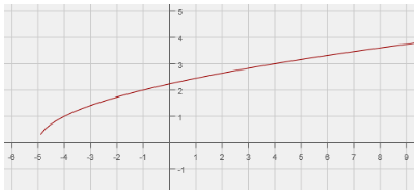
Solution :

The parent function for the given graph is square root function.

y = √x

This parent function is moved to the left of 5 units.

y = √(x - 5)

So, the required function will be 

y = √(x - 5)

Problem 8 :

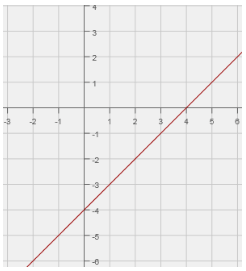
Solution :

The parent function for the given graph is linear function. 

y = x

This parent function is moved down 4 units.

y = x - 4

So, the required function will be 

y = x - 4

Problem 9 :

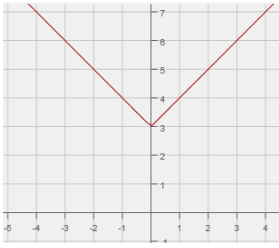
Solution :

The parent function for the given graph of absolute value function.

y = |x|

This parent function is moved 3 units up.

y = |x| + 3

So, the required function will be 

y = |x| + 3

Problem 10 :

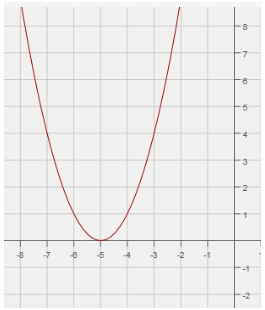
Solution :

The given graph is in the form of u, so it must be a quadratic function.

f(x) = x²

Moving the graph 5 units left.

f(x) = (x - (-5))²

f(x) = (x + 5)²

So, the required function will be 

f(x) = (x + 5)²