HOW TO WRITE LINEAR FUNCTION FROM GRAPH
Using any of the formulas given below, we can find the equation of linear function.
i) Slope intercept form, y = mx + b
ii) Point slope form, (y - y1) = m(x - x1)
Slope = (y2 - y1) / (x2 - x1)
The raising line will have positive slope, the falling line will have negative slope.
(x1, y1) is one of the points lie on the line.
use the graph to write an equation of the line and interpret the slope
Problem 1 :
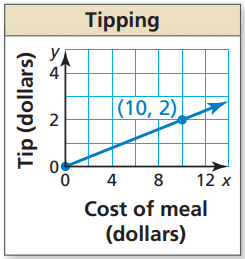
Solution :
From the given figure above, by marking two points we get (0, 0) and (10, 2).
Slope = (y2 - y1) / (x2 - x1)
= (2 - 0) / (10 - 0)
= 2/10
= 1/5
Interpreting the slope :
For every $5 increase of cost of meal, there will be $1 increase in tip.
Problem 2 :
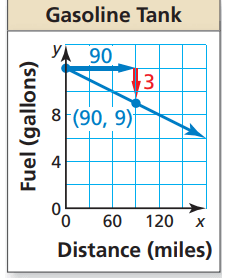
Solution :
From the given figure rise = 3, run = 90
Falling line will have negative slope.
Slope = Rise / Run
= -3/90
= -1/30
Interpreting the slope :
So, car using 1 gallon of gasoline for every 30 miles.
Problem 3 :
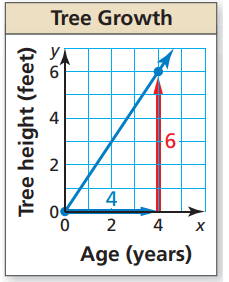
Solution :
From the given figure rise = 6, run = 4
Raising line will have positive slope.
Slope = Rise / Run
= 6/4
= 3/2
Interpreting the slope :
For every 2 years increase, the tree will grow 3 feet.
Problem 4 :
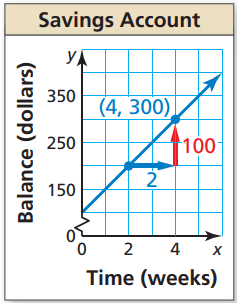
Solution :
From the given figure rise = 100, run = 2
Raising line will have positive slope.
Slope = Rise / Run
= 100/2
= 50/1
Interpreting the slope :
For every 1 week increase, balance will increase $50.
Problem 5 :
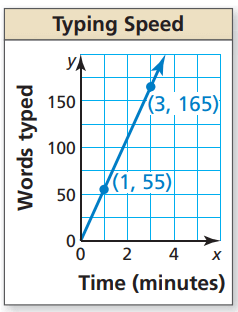
Solution :
Selecting two points from the straight line, let (1, 55) and (3, 165).
Raising line will have positive slope.
Slope = (y2 - y1) / (x2 - x1)
= (165 - 55) / (3 - 1)
= 110/2
= 55/1
Interpreting the slope :
For every 1 minute, she will type 55 words.
Problem 6 :
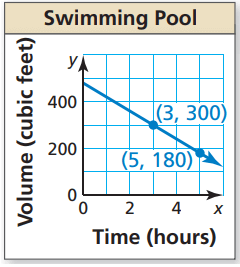
Solution :
Selecting two points from the straight line, let (3, 300) and (5, 180).
Falling line will have negative slope.
Slope = (y2 - y1) / (x2 - x1)
= (180 - 300) / (5 - 3)
= -120 / 2
= -60/1
Interpreting the slope :
For every 1 hour, the volume will decrease at the rate of 60 cubic feet.
Problem 6 :
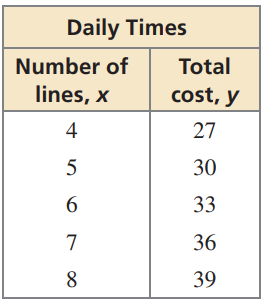
Two newspapers charge a fee for placing an advertisement in their paper plus a fee based on the number of lines in the advertisement. The table shows the total costs for different length advertisements at the Daily Times.
The total cost y (in dollars) for an advertisement that is x lines long at the Greenville Journal is represented by the equation
y = 2x + 20.
a) Which newspaper charges less per line?
b) How many lines must be in an advertisement for the total costs to be the same?
Solution :
Choosing two points from the table, say (4, 27) and (5, 30)
Slope = (y2 - y1) / (x2 - x1)
= (30 - 27) / ( 5 - 1)
= 3/1
Rate of change in daily times = 3
Applying the slope in y = mx + b, we get
y = 3x + b
Choosing one of the points from the table say (6, 33)
33 = 3(6) + b
33 = 18 + b
b = 33 - 18
b = 15
y = 3x + 15
Comparing the given equation y = 2x + 20 with y = mx + b
m = 2
Rate of change for Greenville = 2
a) Cost of Green ville is charging less per line.
b) When the total cost will be same,
y = 3x + 15 ----(1)
y = 2x + 20 ----(2)
(1) = (2)
3x + 15 = 2x + 20
3x - 2x = 20 - 15
x = 5
When the number of lines is 5, then the cost will be equal.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling