HOW TO TELL IF FUNCTION IS EXPONENTIAL GROWTH OR DECAY

From the given graph how to check if it is growth or decay ?

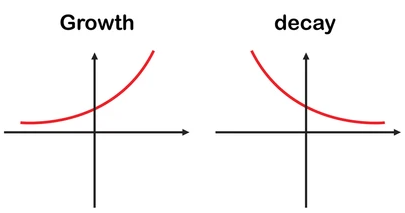
• While observing the graph from left to right, if it goes up, then it will be exponential growth function.
• While observing the graph from left to right, if it goes down, then it will be exponential decay function.

Tell whether the equation or graph represents an exponential growth or exponential decay function.

Problem 1 :

y = 5(0.4)^x

Solution:

y = a(b)^x

a = 5

b = 0.4

0 < b < 1

So, it is exponential decay function.

Problem 2 :

y = -3(7/2)^x

Solution:

y = a(b)^x

a = -3

b = 7/2 = 3.5

b > 1

So, it is exponential growth function.

Problem 3 :

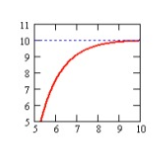
Solution:

While observing the graph from left to right, it goes up. Then it must be exponential growth function.

Problem 4 :

y = 9(1.5)^x 

Solution:

y = a(b)^x

a = 9

b = 1.5

b > 1

So, it is exponential growth function.

Problem 5 :

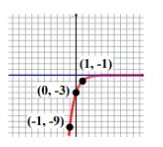
Solution:

By observing the graph, it goes up. So, it is increasing function.

initial value a is -3.

y = ab^x ---(1)

Choosing the point (-1, -9) and applying in the function, we get

y = -3 b^x 

-9 = -3 b^-1 

-9 = -3 (1/b)

3 = 1/b

b = 1/3

By applying all the values in (1), we get

y = -3(1/3)^x

By considering the base it must be exponential decay, but there must be a reflection since we have negative coefficient.

Problem 6 :  

y = 0.2(0.3)^-x

Solution:

Here b = 0.3 which is in between 0 and 1. But we have negative in the power.

y = 0.2(3/10)^-x

y = 0.2(10/3)^x

10/3 is greater than 1, so it is exponential growth function.

Problem 7 :

y = -3(6)^x

Solution:

y = a(b)^x

a = -3

b = 6

b > 1

So, it is exponential growth function.

Problem 8 :

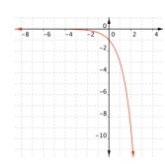
Solution:

By observing the graph from left to right, it goes down. So, it is exponential decay function.