HOW TO TELL IF FUNCTION IS EVEN OR ODD FROM GRAPH
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A Function can be classified as Even, Odd or Neither. This classification can be determined graphically or algebraically.
How to check if the graph is odd ?
The graph will be symmetric with respect to the origin.
In other words :
If you spin the picture upside down about the Origin, the graph looks the same!
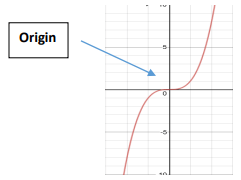
How to check if the graph is even ?
The graph will be symmetric with respect to the y-axis.
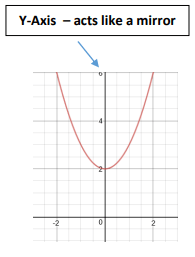
Properties of odd and even functions :
Properties of odd function :
- The graph is symmetric about origin.
- The exponents of all terms in its equation are odd.
Properties of even function :
- The graph is symmetric about y-axis.
- The exponents of all terms in its equation are even.
Graphically determine whether the following functions are Even, Odd, or Neither
Problem 1 :
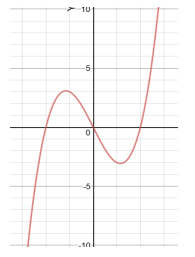
Solution :
The graph is symmetric about origin. So, it is odd function.
Problem 2 :
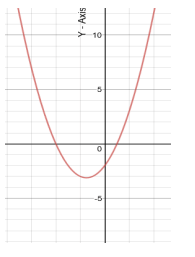
Solution :
The graph is not symmetric about origin, then it is not odd function.
The graph is not symmetric about y-axis, then it is not even function.
So, it is neither.
Problem 3 :
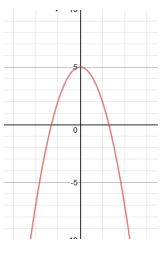
Solution :
Here y-axis is acting as a mirror. Clearly it is symmetric about y-axis. Then, it is even function.
Problem 4 :
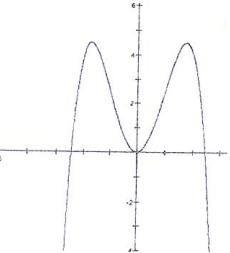
Solution :
The graph is symmetric about origin. So, it is odd function.
Problem 5 :
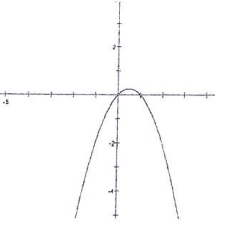
Solution :
The graph is not symmetric about origin, then it is not odd function.
The graph is not symmetric about y-axis, then it is not even function.
So, it is neither.
Problem 6 :
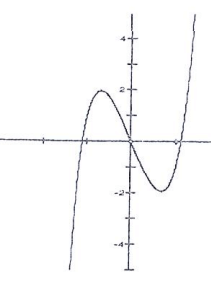
Solution :
The graph is symmetric about origin. So, it is odd function.
Problem 7 :
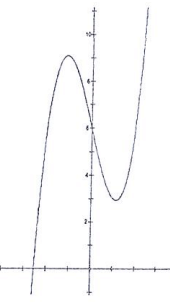
Solution :
The graph is not symmetric about origin, then it is not odd function.
The graph is not symmetric about y-axis, then it is not even function.
So, it is neither.
Algebraically testing whether it is even odd or neither
For each of the following functions, classify each as: even, odd or neither. You must show your work to prove your classification.
Problem 8 :
f(x) = x2 - 2x
Solution :
f(x) = x2 - 2x
Put x = -x
f(-x) = (-x)2 - 2(-x)
= x2 + 2x
So, it is neither.
Problem 9 :
f(x) = 3x5 - 4x
Solution :
f(x) = 3x5 - 4x
Put x = -x
f(-x) = 3(-x)5 - 4(-x)
= -3x5 + 4x
Factoring the negative, we get
= -(3x5 - 4x)
f(-x) = -f(x)
So, it is odd function.
Problem 10 :
Solution :
So, it is even function.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling