HOW TO SOLVE INVERSE TRIGONOMETRIC EQUATIONS

Solve :

Problem 1 :

Solution :

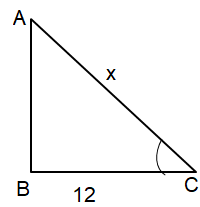Adjacent side = 12 hypotenuse = x Opposite side = √x2 - 122 = √(x2 - 144)

Writing cos^-1 as sin^-1, we get

Problem 2 :

Solution :

Problem 3 :

Solution :

Problem 4 : 

Solution :

From cot^-1x, using reference triangle.

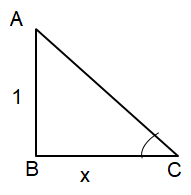Adjacent side = x opposite side = 1 tan-1x = 1/x

From cot^-1(x+2), using reference triangle.

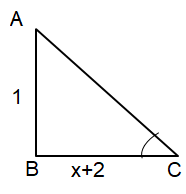Adjacent side = x+2 opposite side = 1 tan-1x = 1/(x+2)

Problem 5 :

Find the number of solutions of the equation

Solution :

By simplifying this, we will get a cubic polynomial. By solving the cubic polynomial, we will receive 3 solutions.

So, the number of solutions of the equation is 3.