HOW TO SKETCH THE GRAPH OF ASBOLUTE VALUE FUNCTION

To graph absolute value function, we have to find the following characteristics of the given function.

(i) Find vertex

(ii)  x - intercepts (roots, zeroes, solutions) and y - intercept

(iii) Slope and Reflections (or) Direction of opening

(iv)  Domain and Range

(v)  Increasing/decreasing interval

To get clear definition, please click on the link below.

Graphing absolute value function

Graph the following absolute value function :

Problem 1 :

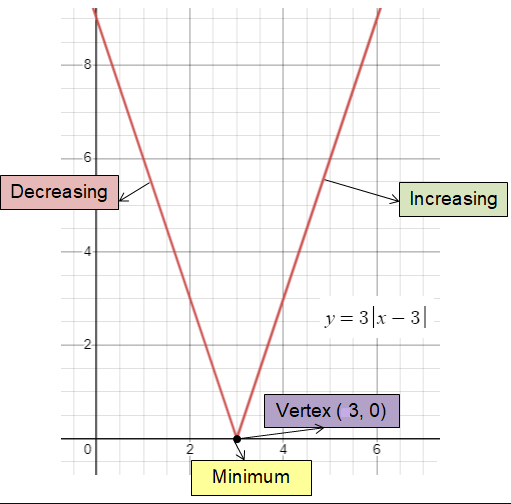
y = 3|x - 3|

Solution :

Finding vertex :

y = 3|x - 3|

Comparing with y = a|x - h| + k

y = 3|x - 3| + 0

Vertex is at (3, 0).

x and y-intercepts :

x-intercept, put y = 0

3|x - 3| = 0

Since we have zero on the right side, don't have to decompose it into two branches.

|x - 3| = 0

x = 3

x-intercept is (3, 0).

y-intercept, put x = 0

y = 3|0 - 3|

y = 3(3)

y = 9

y-intercept is at (0, 9).

Slope : 

a = 3

The curve will open up.

Domain and range :

• All real values is domain.
• Range is 3 ≤ y ≤ ∞

Increasing and Decreasing :

• To the left of minimum, it is decreasing.
• To the right of minimum, it is increasing.

Problem 2 :

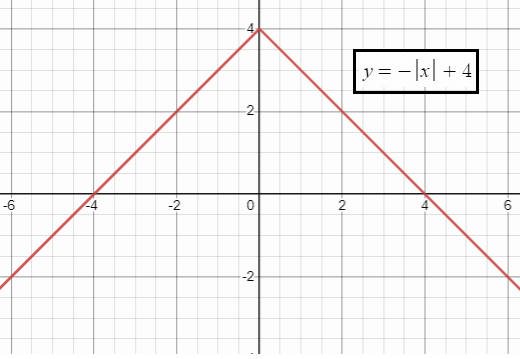
y = -|x| + 4

Solution :

Finding vertex :

y = -|x| + 4

Comparing with y = a|x - h| + k

y = -1 |x - 0| + 4

Vertex is at (0, 4).

x and y-intercepts :

x-intercept, put y = 0

-|x| + 4 = 0

-|x| = -4

|x| = 4

x = 4 and x = -4

x-intercepts are (4, 0) and (-4, 0).

y-intercept, put x = 0

y = -|0| + 4

y = 4

y-intercept is at (0, 4).

Slope : 

Slope (a) = -1

The curve will open down.

Domain and range :

• All real values is domain.
• Range is 4 ≤ y ≤ -∞

Increasing and Decreasing :

• To the left of maximum, it is increasing.
• To the right of maximum, it is decreasing.

Problem 3 :

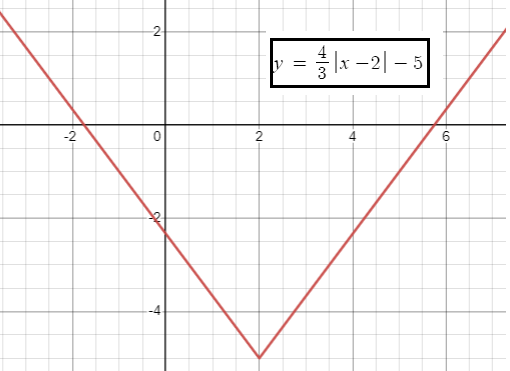
y = (4/3) |x + 2| - 5

Solution :

Finding vertex :

y = (4/3) |x + 2| - 5

Comparing with y = a|x - h| + k

y = (4/3) |x + 2| - 5

Vertex is at (-2, -5).

x and y-intercepts :

x-intercept, put y = 0

(4/3) |x + 2| - 5 = 0

(4/3)|x + 2| = 5

|x + 2| = 5(3/4)

|x + 2| = 15/4

x-intercept is at (7/4, 0) and (-19/2, 0).

y-intercept, put x = 0

y = (4/3) |0 + 2| - 5

y = (8/3) - 5

y = -7/3

y-intercept (0, -7/3).

Slope :

Slope (a) = 4/3

The curve will open up.

Domain and range :

• All real values is domain.
• Range is 4 ≤ y ≤ -∞

Increasing and Decreasing :

• To the left of minimum, it is decreasing.
• To the right of minimum, it is increasing.

Problem 4 :

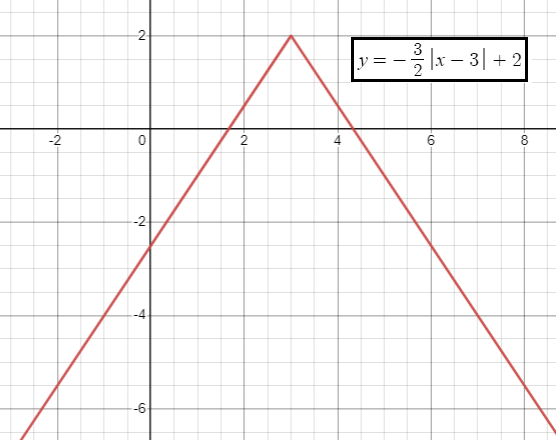
y = -(3/2) |x - 3| + 2

Solution :

Finding vertex :

y = -(3/2) |x - 3| + 2

Comparing with y = a|x - h| + k

y = -(3/2) |x - 3| + 2

Vertex is at (3, 2).

x and y-intercepts :

x-intercept, put y = 0

-(3/2) |x - 3| + 2 = 0

-(3/2) |x - 3| = -2

(3/2) |x - 3| = 2

|x - 3| = 4/3

x-intercept is at (13/3, 0) and (5/3, 0).

y-intercept, put x = 0

y = -(3/2) |0 - 3| + 2

y = -9/2 + 2

y = -5/2

y-intercept is (0, -5/2).

Slope :

Slope (a) = -3/2

The curve will open down.

Domain and range :

• All real values is domain.
• Range is 2 ≤ y ≤ -∞

Increasing and Decreasing :

• To the left of maximum, it is increasing.
• To the right of maximum, it is decreasing.