HOW TO KNOW IF THE EXPONENTIAL FUNCTION IS GROWTH OR DECAY

Exponential function will be in the form

y = ab^x-h + k

From the equation given, how to check if it is growth or decay ?

Here the value of b will decide whether the function is exponential growth or decay.

• If b > 1, then it is exponential growth function.
• If b lies in between 0 and 1, then it is exponential decay function.

y = 3(2)x y = 3(1/2)x

2 > 1, it is exponential growth 0 < 1/2 < 1, it is exponential decay

From the graph given, how to check if it is growth or decay ?

Exponential growth :

By observing the graph from left to right, it is going up. Then , it is exponential growth function.

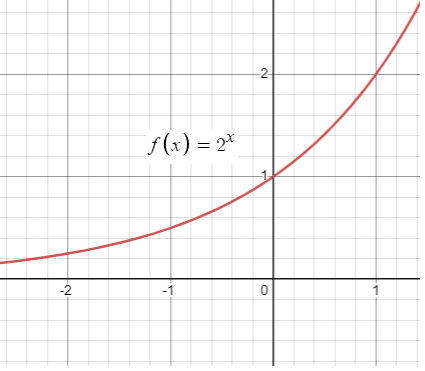
Exponential decay :

By observing the graph from left to right, it is going down. Then , it is exponential decay function.

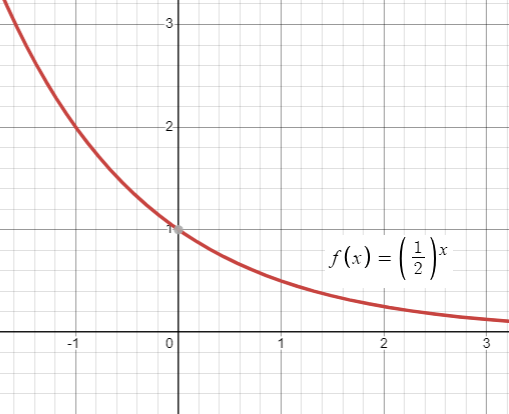
Classify the function is exponential growth or decay.

Problem 1 :

y = 3(2/7)^x

Solution :

Here a = 3 and b = 2/7, 0 < b < 1

So, it is exponential decay function.

Problem 2 :

y = 8(5/2)^x

Solution :

Here a = 8 and b = 5/2, 0 < b < 1

So, it is exponential decay function.

Problem 3 :

y = (1/4)(3)^x

Solution :

Here a = 1/4 and b = 3, b > 1

So, it is exponential growth function.

Problem 4 :

y = (4/3)(3/5)^x

Solution :

Here a = 4/3 and b = 3/5, b < 1

So, it is exponential decay function.

Problem 5 :

Each day, 10% of a certain drug dissipates from the system.

a. Classify the function representing this situation as either exponential growth or decay, and identify the growth or decay factor. Then graph the function.

b. How much of the original amount remains in the system after 9 days?

c. If a second dose should not be taken if more than 50% of the original amount is in the system, when should the label say it is safe to redose?

Design the label and explain your reasoning.

Solution :

Each day, the quantity of drug dissipates. Then, it must be exponential decay function.

a.  The original quantity of drug be 100%, decreasing rate is 10%

The required function will be y = a(1 - r%)^x

Initial value = 100

y = 100(1 - 10%)^x

y = 100(90%)^x

y = 100(0.90)^x

Where x is the number of days.

b.  After 9 days.

y = 100(0.90)⁹

y = 38.74

Quantity of drug remaining = 100 - 38.74

= 61.26

c.

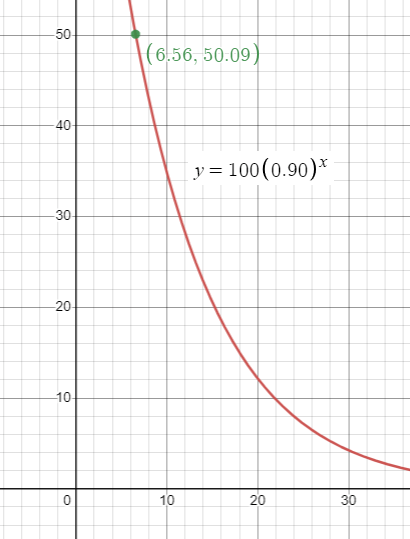
So, approximately after 7th day it is safe to redose.

Problem 6 :

The function P(x) = 2.28(0.9)^x can be used to model the number of pay phones in millions x years since 1999.

a. Classify the function representing this situation as either exponential growth or decay, and identify the growth or decay factor. Then graph the function.

b. Explain what the P(x)-intercept and the asymptote represent in this situation

Solution :

P(x) = 2.28(0.9)^x

Here b = 0.9 < 1, then it is exponential decay function.

To draw the graph, we find y-intercept and asymptote :

To find y-intercept, we apply x = 0

P(0) = 2.28(0.9)⁰

= 2.28(1)

= 2.28

Horizontal asymptote :

y = 0 or x-axis

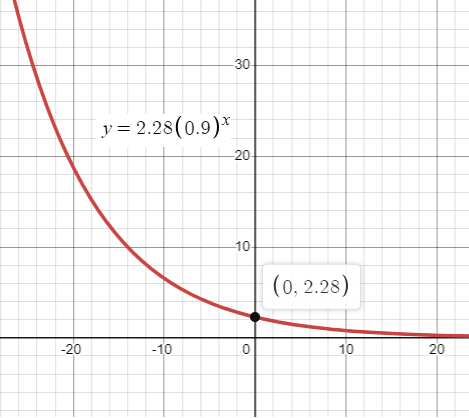
b. y-intercept is 2.28 when x = 0

(0, 2.28)

Horizontal asymptote is y = 0

The number of pay phones can approach 0, but will never equal 0. This makes sense as there will probably always be a need for some pay phones

Problem 7 :

A sequence of numbers follows a pattern in which the next number is 125% of the previous number. The first number in the pattern is 18.

a. Write the function that represents the situation.

b. Classify the function as either exponential growth or decay, and identify the growth or decay factor. Then graph the function for the first 10 numbers.

c. What is the value of the tenth number? Round to the nearest whole number.

Solution :

a) The initial value = 18

Fist number = 18

Second number = 125% of 18

Third number = 125% of (125% of 18)

= 1.25 (1.25 x 18)

= 18(1.25)²

Fourth number will be 18(1.25)³

In this way, to find the nth number we will use the formula

18(1.25)^n-1

b) Growth factor :

= 18(1.25)^n-1

Here b = 1.25 > 1, it is growth function and its growth factor will be 1.25.

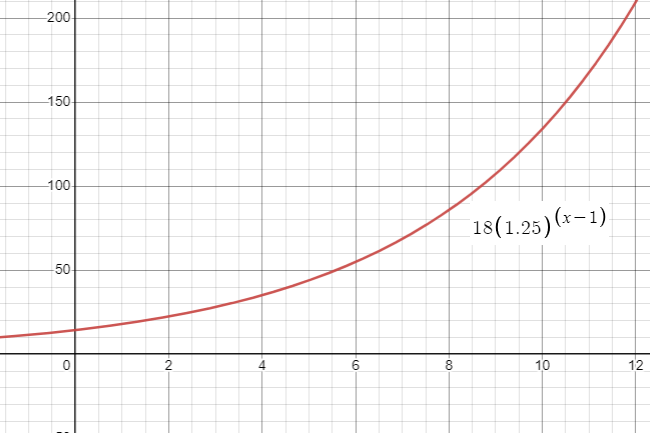
c) Finding the 10^th number :

= 18(1.25)^{10 - 1}

= 18(1.25)⁹

= 18(7.45)

= 134.11

10^th term of the pattern is 134.

Problem 8 :

A substance decays 35% each day. After 8 days, there are 8 milligrams of the substance remaining. How many milligrams were there initially?

Solution :

Let us consider 100% of substance initially.

Every day 35% decays.

P(x) = a(1 - r%)^x

= a(1 - 35%)^x

p(x) = a(0.65)^x

8 = a(0.65)⁸

8/0.0318 = a

a = 251.5

a = 252 milligram

So, there was 252 milligrams of substance initially.