HOW TO KNOW IF A GRAPH TO KNOW IF A GRAPH IS DISCRETE OR CONTINOUS

Graph of discrete function :

In the graph of discrete functions only separate and distinct points are plotted, and only these points have meaning of the original problem.

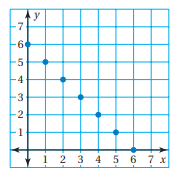
The graph is a series of unconnected points (a scatter plot).

Graph of continuous function :

In the graph of a continuous function, the points are connected with continuous line, since every point has meaning to the original problem.

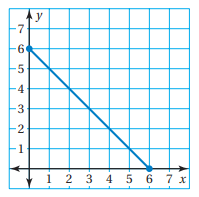
Tell whether the relation is a function.

Identify the following,

i)  Domain

ii) Range. 

iii)  Identity if its discrete or continuous.

Problem 1 :

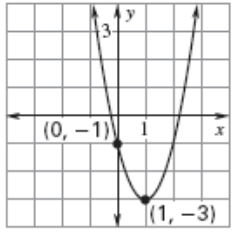
Solution :

Using the vertical line test, the vertical line will intersect the curve at one point. So, it is a function.

Domain :

All real values of x.

Range :

1 ≤ y < ∞

Type of function :

It is continuous function.

Problem 2 :

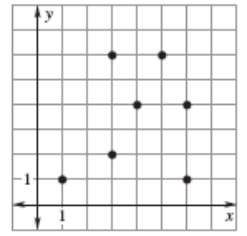
Solution :

By observing the points, input 3 is having more than one output. So, it is not a function.

Writing the points plotted as ordered pair, we get

(1, 1) (3, 2) (3, 6) (4, 4) (5, 6) (6, 1) and (6, 4)

Domain :

 {1, 3 ,4, 5, 6}

Range :

{1, 2, 4, 6}

Problem 3 :

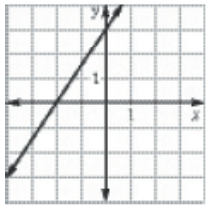
Solution :

Drawing the vertical line, it will intersect the graph maximum at one point. So, it is a function.

Domain :

All real values of x.

Range :

All real value of y.

Type of function :

It is continuous function.

Problem 4 :

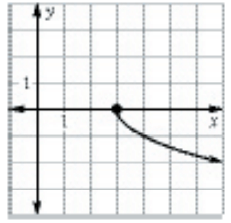
Solution :

Drawing the vertical line, it will intersect the graph maximum at one point. So, it is a function.

Domain :

3 ≤ x < ∞

Range :

0 ≤ y < ∞

Type of function :

It is continuous function.

Problem 5 :

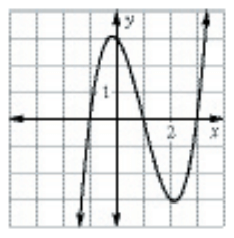
Solution :

Drawing the vertical line, it will intersect the graph maximum at one point. So, it is a function.

Domain :

All real values of x.

Range :

All real values of y.

Type of function :

It is continuous function.

Problem 6 :

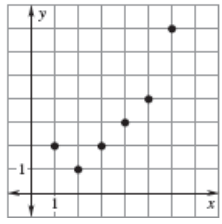
Solution :

By observing the points plotted. Every point is having one output maximum. So, it is a function. By writing points as ordered pairs, we get

{(1, 2) (2, 1) (3, 2) (4, 3)(5, 4) (6, 6)}

Domain :

{1, 2, 3, 4, 5, 6}

Range :

{1, 2, 3, 4, 6}

Type of function :

It is discrete function.

Problem 7 :

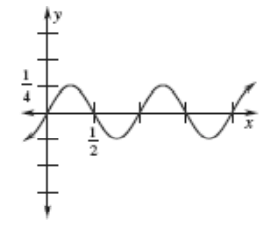
Solution :

Vertical line will intersect the curve at one point maximum. So, it is a function.

Domain :

All real values of x.

Range :

From the graph given it is clear, the minimum and maximum value of y are -1/4 and 1/4 respectively. So, the range is 

-1/4 ≤ y ≤ 1/4

Type of function :

It is continuous function.

Problem 8 :

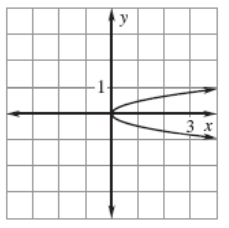
Solution :

Vertical line will intersect the curve at two points. So, it is not  a function.

Domain :

0 ≤ x ≤ ∞

Range :

All real value of y.

Problem 9 :

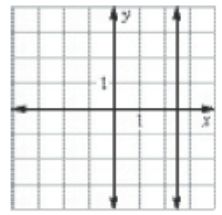
Solution :

The same input is associated with many outputs, it is not a function.