HOW TO FIND VERTICAL ASYMPTOTE OF COTANGENT FUNCTION

We use the characteristics of the cotangent curve to graph tangent functions of the form y = A cot (Bx- C), where B > 0

Step 1 :

Find two consecutive asymptotes by finding an interval containing one period.

A pair of consecutive asymptotes occurs at 

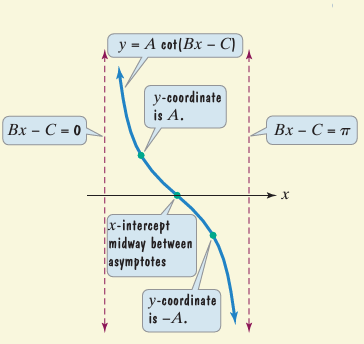
Step 2 :

cot x = cos x / sin x

Here sin x = k𝜋

In the given function, by equation BX - C to k𝜋 and applying the value of k, we can get more asymptotes.

Problem 1 :

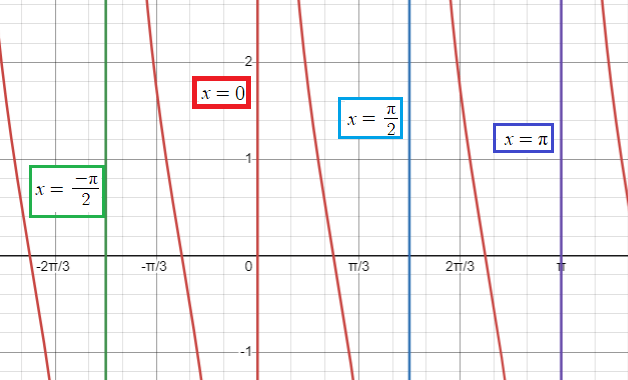
Graph y = 3 cot 2x

Solution :

• A = 3, B = 2
• period = 𝜋/|B|
• period for the function y = 3 cot 2x is (0, 𝜋/2)

Step 1 :

Find two consecutive asymptotes, we do this by finding an interval containing one period.

An interval containing one period is (0, 𝜋/2). Thus two consecutive asymptotes occur at x = 0 and x = 𝜋/2.

Step 2 :

Vertical asymptote of y = cot x is k𝜋, where k is integer. Here

2x = k𝜋

x = k𝜋/2

• When k = -1, x = -𝜋/2
• When k = 0, x = 0
• When k = 1, x = 𝜋/2
• When k = 2, x = 𝜋

Problem 2 :

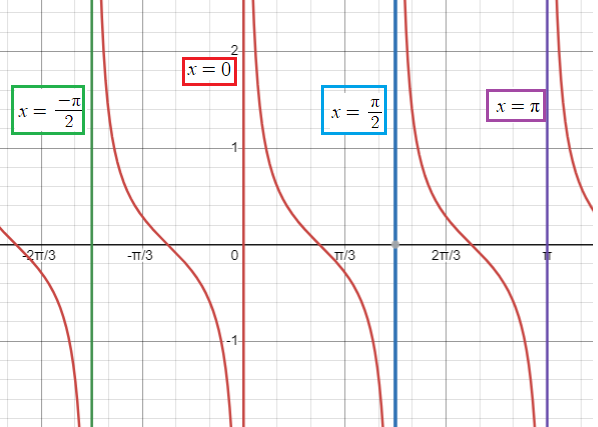
Graph y = (1/2) cot 2x

Solution :

• A = 1/2, B = 2
• period = 𝜋/|B|
• period for the function y = (1/2) cot 2x is (0, 𝜋/2)

Step 1 :

Find two consecutive asymptotes, we do this by finding an interval containing one period.

An interval containing one period is (0, 𝜋/2). Thus two consecutive asymptotes occur at x = 0 and x = 𝜋/2.

Step 2 :

Vertical asymptote of y = cot x is k𝜋, where k is integer. Here

2x = k𝜋

x = k𝜋/2

• When k = -1, x = -𝜋/2
• When k = 0, x = 0
• When k = 1, x = 𝜋/2
• When k = 2, x = 𝜋

Problem 3 :

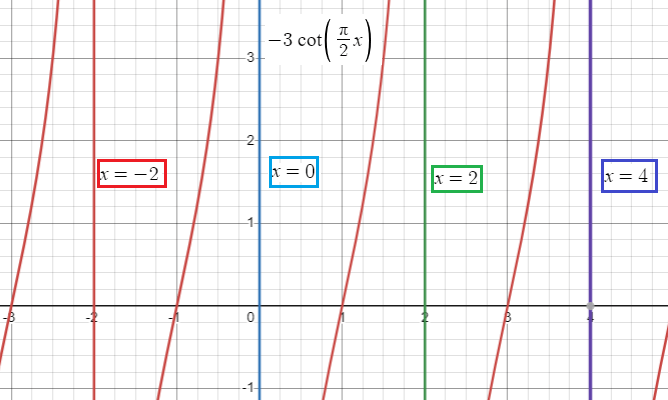
Graph y = -3 cot (𝜋/2)x

Solution :

• A = 3, B = 1/2
• period = 𝜋/|B|
• period for the function y =  -3 cot (𝜋/2)x is (0, 2)

Step 1 :

Find two consecutive asymptotes, we do this by finding an interval containing one period.

An interval containing one period is (0, 2). Thus two consecutive asymptotes occur at x = 0 and x = 2.

Step 2 :

Vertical asymptote of y = cot x is k𝜋, where k is integer. Here

(𝜋/2)x = k𝜋

x = k𝜋/(𝜋/2)

x = 2k

• When k = -1, x = -2
• When k = 0, x = 0
• When k = 1, x = 2
• When k = 2, x = 4

Repeat the same pattern in the interval.

Problem 4 :

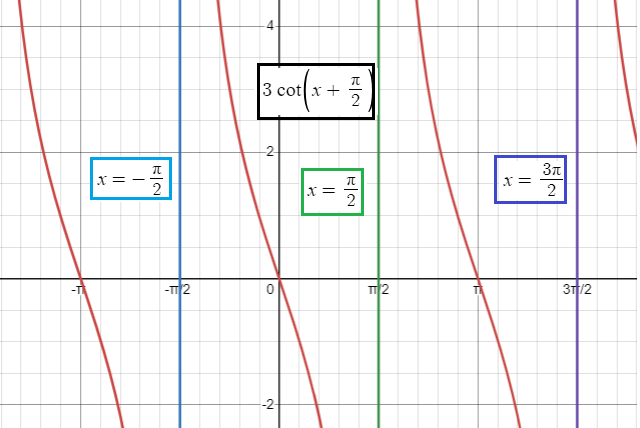
Graph y = 3 cot (x + 𝜋/2)

Solution :

• A = 3, B = 1
• period = 𝜋/|B| == > 𝜋
• period for the function y = 3 cot (x + 𝜋/2) is (0, 𝜋)

Step 1 :

Find two consecutive asymptotes, we do this by finding an interval containing one period.

An interval containing one period is (-𝜋/2, 𝜋/2). Thus two consecutive asymptotes occur at x = -𝜋/2 and x = 𝜋/2.

Step 2 :

Vertical asymptote of y = cot x is k𝜋, where k is integer. Here

x+𝜋/2 = k𝜋

x = k𝜋 - (𝜋/2)

x = (2k𝜋 - 𝜋)/2

x = (𝜋/2)(2k-1)

• When k = 0, x = -𝜋/2
  
• When k = 1, x = 𝜋/2
• When k = 2, x = 3𝜋/2

Repeat the same pattern in the interval.

Problem 5 :

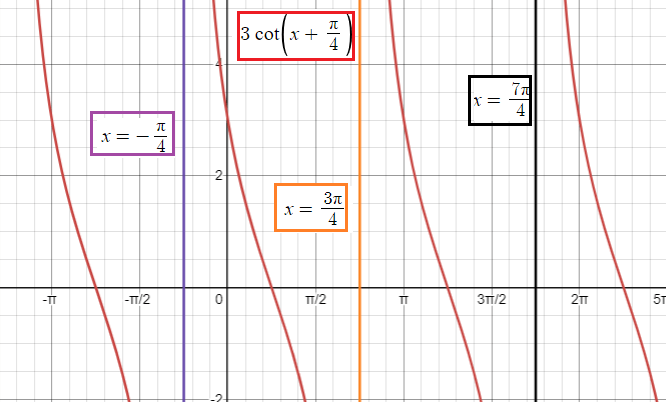
Graph y = 3 cot (x + 𝜋/4)

Solution :

• A = 3, B = 1
• period = 𝜋/|B| == > 𝜋
• period for the function y = 3 cot (x + 𝜋/4) is (0, 𝜋)

Step 1 :

Find two consecutive asymptotes, we do this by finding an interval containing one period.

An interval containing one period is (-𝜋/4, 3𝜋/4). Thus two consecutive asymptotes occur at x = -𝜋/4 and x = 3𝜋/4.

Step 2 :

Vertical asymptote of y = cot x is k𝜋, where k is integer. Here

(x + 𝜋/4)= k𝜋

x = k𝜋 - (𝜋/4)

x = (4k𝜋 - 𝜋)/4

x = (𝜋/4)(4k-1)

• When k = 0, x = -𝜋/4
  
• When k = 1, x = 3𝜋/4
• When k = 2, x = 7𝜋/4

Repeat the same pattern in the interval.

Problem 6 :

In order to graph y = 3 cot (𝜋/2) x, an interval containing one period is found by solving 0 < (𝜋/2)x < 𝜋. 

An interval containing one period is two consecutive asymptotes occur at x = and x = .

Solution :

• A = 3, B = 𝜋/2
• period = 𝜋/|B| == > 2
• period for the function y = y = 3 cot (𝜋/2) x is (0, 2)

An interval containing one period is (0, 2). Thus two consecutive asymptotes occur at x = 0 and x = 2.

Vertical asymptote of y = cot x is k𝜋, where k is integer. Here

(𝜋/2)x = k𝜋

x = k𝜋 x (2/𝜋)

x = 2k

• When k = 0, x = 0
• When k = 1, x = 2
• When k = 2, x = 4