HOW TO FIND VERTICAL ASYMPTOTE OF SEC CSC AND TAN FUNCTIONS

To find vertical asymptote of any rational function, we will equate the denominator to 0.

Graph of cosec x and its vertical asymptote :

cosec x = 1/sin x, where sin x ≠ 0

Cosec is the reciprocal of sine function.

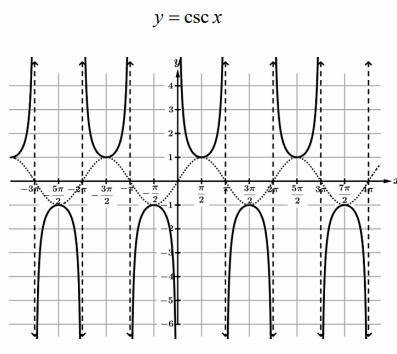
The graph of y = csc x has vertical asymptotes where sin x x = 0

x = k𝜋, where k is an integer.

Graph of sec x and its vertical asymptote :

sec x = 1/cos x, where cos x ≠ 0

Secant is the reciprocal of cosine function.

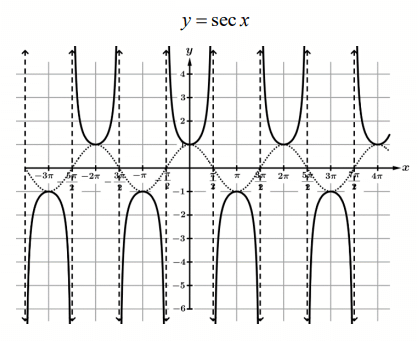
The graph of y = sec x has vertical asymptotes where cos x = 0

Where k is an integer.

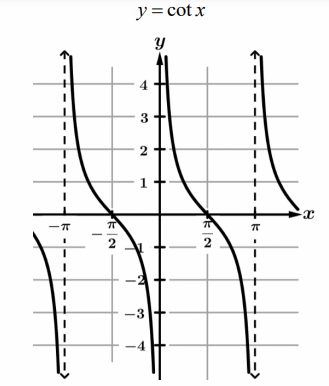
Graph of tan x and its vertical asymptote :

tan x = sin x/cos x, where cos x ≠ 0

The graph of y = tan x has vertical asymptotes where sin x x = 0

x = k𝜋, where k is an integer.

Problem 1 :

Let f(x) = 3 sec 2x, which of the following is the vertical asymptote on the graph f ?

a) x = π        b) x = 3π/2      c)  x = π/4      d) x = 0

Solution :

f(x) = 3 sec 2x

f(x) = 3 (1/cos 2x)

To find the vertical asymptote, we equate the denominator to 0.

cos 2x = 0

2x = cos ^-1(0)

2x = π/2, 3π/2, ......

x = π/4, 3π/4, ......

Accordingly the given option x = π/4 is the vertical asymptote for the function f(x).

Problem 2 :

Let g(x) = 4 - 2 csc (πx), which of the following is the vertical asymptote on the graph g ?

a) x = π/2        b) x = π       c)  x = 1/2      d) x = 1

Solution :

g(x) = 4 - 2 csc (πx)

g(x) = 4 - 2 (1/sin (πx))

To find the vertical asymptote, we equate the denominator to 0.

sin πx = 0

πx = sin ^-1(0)

πx = 0, π, 2π, ......

x = 0, 1, 2 , ......

Accordingly the given option x = 1 is the vertical asymptote for the function g(x).

Problem 3 :

Let k(x) = -5 cot (2πx), which of the following is the vertical asymptote on the graph k ?

a) x = 1/4        b) x = 1/2       c)  x = π/2      d) x = 2π

Solution :

k(x) = -5 cot (2πx)

= -5(cos (2πx) / sin (2πx))

To find the vertical asymptote, we equate the denominator to 0.

sin 2 πx = 0

2πx = sin ^-1(0)

2πx = kπ

x = k/2

Where k is an integer.

Say k = 1, then x = 1/2

Say k = 2, then x = 2/2 ==> 1

Say k = 3, then x = 3/2 ==> 1.5

Accordingly the given option x = 1/2 is the vertical asymptote for the function k(x).

Problem 4 :

In order to graph y = (1/2) tan 2x, an interval containing one period is found by solving - π/2 < 2x < π/2.

An interval containing one period is two consecutive asymptotes occur at x = and x = .

Solution :

y = (1/2) tan 2x

- π/2 < 2x < π/2

Multiplying by 2, - π < x < π

So, one period of the given function y will lie in the interval (-π, π).

Vertical asymptote :

y = (1/2) tan 2x

y = sin 2x/2cos 2x

2 cos 2x = 0

cos 2x = 0

2x = cos^-1(0)

2x = π/2 + k π

x = π/4 + (kπ/2)

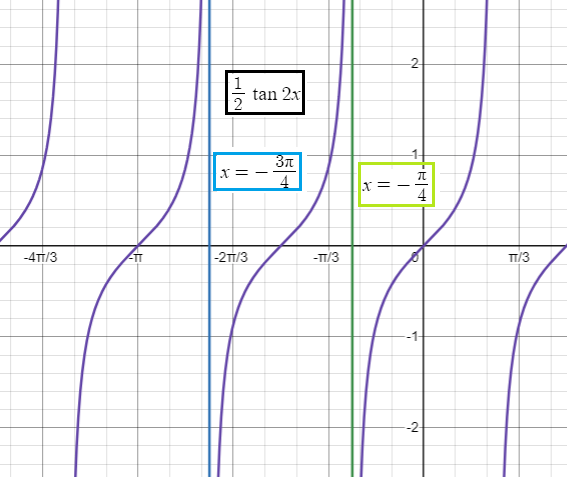
So, consecutive vertical asymptotes are appearing at x = -3π/4 and x = π/4.

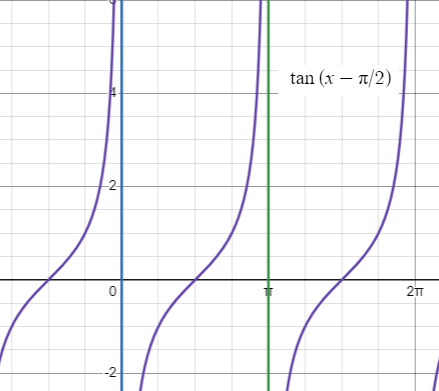
Problem 5 :

An interval containing one period of y = tan (x - π/2) is at x = . Thus, two consecutive asymptotes occur and x = and x = 

Solution :

Since the given function is tangent function, its domain will be odd multiples of π/2

- π/2 < (x - π/2) < π/2

Adding π/2, we get

(-π/2) + (π/2) < x  < π/2 + π/2

0 < x < π

So, one period of the given function y will lie in the interval (0, π).

Vertical asymptote :

y = tan (x - π/2)

y = sin (x - π/2) / cos (x - π/2)

cos (x - π/2) = 0

(x - π/2) = cos^-1(0)

x - π/2 = π/2 + k π

x = (π/2 + π/2) + kπ

x = π + kπ

So, consecutive asymptotes will lie at x = 0 and x = π.