HOW TO FIND VERTEX FOCUS AND DIRECTRIX OF PARABOLA FROM EQUATION
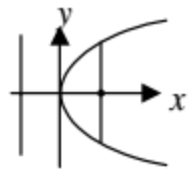
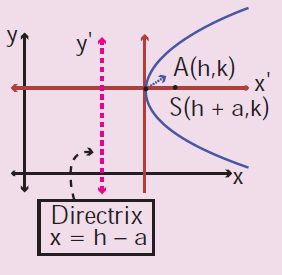
The parabola symmetric about x-axis and it opens rightward.
 |
 |
|
Equation Vertex Focus Latus rectum Directrix Length of latus rectum |
(y - k)2 = 4a(x - h) (h, k) (h + a, k) x = h + a x = h - a 4a |
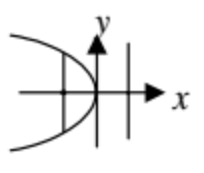
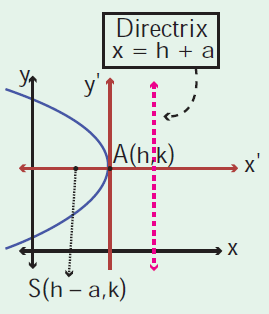
The parabola symmetric about x-axis and it opens leftward.
 |
 |
|
Equation Vertex Focus Latus rectum Directrix Length of latus rectum |
(y - k)2 = -4a(x - h) (h, k) (h - a, k) x = h - a x = h + a 4a |
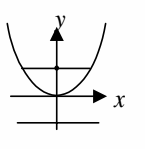
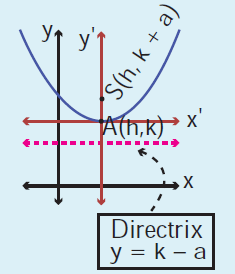
The parabola symmetric about y-axis and it open upward.
 |
 |
|
Equation Vertex Focus Latus rectum Directrix Length of latus rectum |
(x - h)2 = 4a(y - k) (h, k) (h, k + a) y = k + a y = k - a 4a |
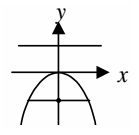
The parabola symmetric about y-axis and it open downward.
 |
 |
|
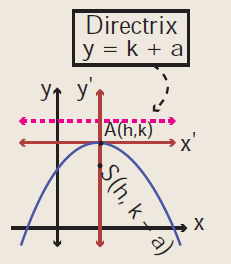Equation Vertex Focus Latus rectum Directrix Length of latus rectum |
(x - h)2 = -4a(y - k) (h, k) (h, k - a) y = k - a y = k + a 4a |
Identify the coordinates of
- vertex
- focus
- the equations of the axis of symmetry
- latus rectum
- directrix
- the direction of opening of the parabola
with the given equation. Then find the length of latus rectum and graph the parabola.
Problem 1 :
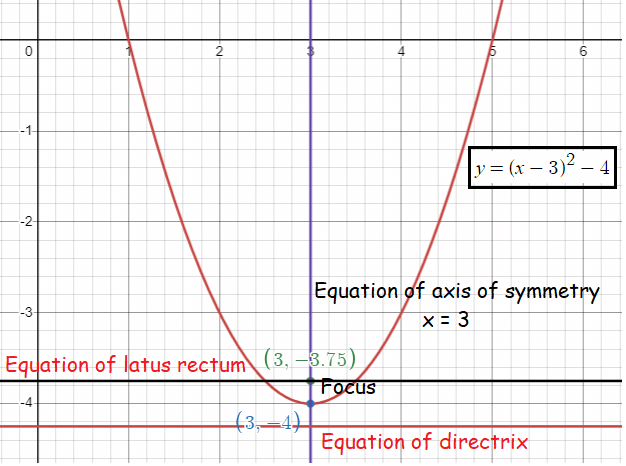
y = (x - 3)2 - 4
Solution :
y = (x - 3)2 - 4
(x - 3)2 = (y + 4)
4a = 1
a = 1/4
Comparing with (x - h)2 = 4a(y - k), we know that the parabola is symmetric about y axis and opening up.
|
Direction of opening |
Opening up |
|
Vertex |
(h, k) ==> (3, -4) |
|
Focus |
(h, k + a) ==> (3, -4 + 1/4) (3, -15/4) |
|
Equation of latus rectum |
y = k + a y = -4 + 1/4 = -15/4 |
|
Equation of directrix |
y = k - a y = -4 - (1/4) y = -17/4 |
|
Equation of axis of symmetry |
x = h x = 3 |
|
Length of latus rectum |
4a = 1 1 unit |
Problem 2 :
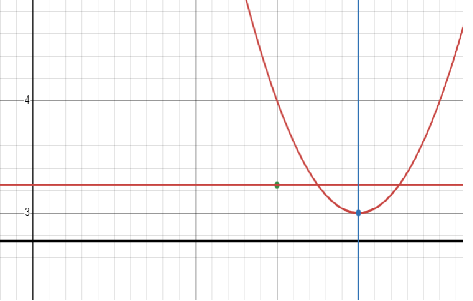
y = (x - 4)2 + 3
Solution :
y = (x - 4)2 + 3
(x - 4)2 = (y - 3)
4a = 1
a = 1/4
Comparing with (x - h)2 = 4a(y - k), we know that the parabola is symmetric about y axis and opening up.
|
Direction of opening |
Opening up |
|
Vertex |
(h, k) ==> (4, 3) |
|
Focus |
(h, k + a) ==> (4, 3 + 1/4) (3, 13/4) |
|
Equation of latus rectum |
y = k + a y = 3 + 1/4 = 13/4 |
|
Equation of directrix |
y = k - a y = 3 - (1/4) y = 11/4 |
|
Equation of axis of symmetry |
x = h x = 4 |
|
Length of latus rectum |
4a = 1 unit |
Problem 3 :
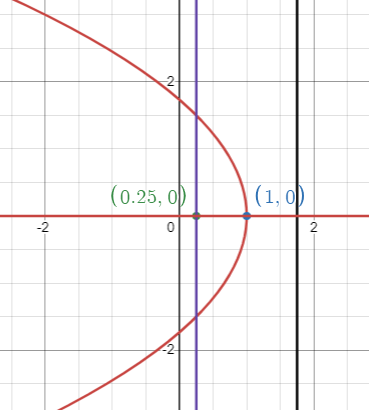
x = (-1/3) y2 + 1
Solution :
x = (-1/3) y2 + 1
x - 1 = (-1/3) y2
y2 = -3(x - 1)
Comparing with y2 = 4a(x - h), we know that the parabola is symmetric about x axis and it opens leftward.
4a = 3
a = 3/4
|
Direction of opening |
Opening up |
|
Vertex |
(h, k) ==> (1, 0) |
|
Focus |
h - a = 1 - (3/4) = 1 - 3/4 = 1/4 (h - a, k) ==> (1/4, 0) |
|
Equation of latus rectum |
x = h - a x = 1 - 3/4 = 1/4 |
|
Equation of directrix |
x = h + a x = 1 + (3/4) x = 7/4 |
|
Equation of axis of symmetry |
y = k y = 0 |
|
Length of latus rectum |
4a = 3 units |
Problem 4 :
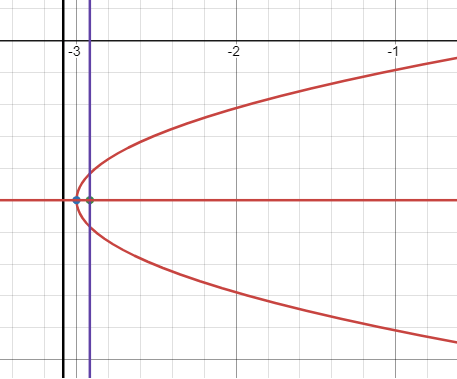
x = 3(y + 1)2 - 3
Solution :
x = 3(y + 1)2 - 3
x + 3 = 3 (y + 1)2
(y + 1)2 = (1/3) (x + 3)
Comparing with (y - k)2 = 4a(x - h), we know that the parabola is symmetric about x axis and it opens rightward.
4a = 1/3
a = 1/12
|
Direction of opening |
Opening up |
|
Vertex |
(h, k) ==> (-3, -1) |
|
Focus |
h + a = -3 + (1/12) = -35/12 (h + a, k) ==> (-35/12, -1) |
|
Equation of latus rectum |
x = h + a x = -35/12 |
|
Equation of directrix |
x = h - a x = -3 - (1/12) x = -37/12 |
|
Equation of axis of symmetry |
y = k y = -1 |
|
Length of latus rectum |
4a = 1/3 units |
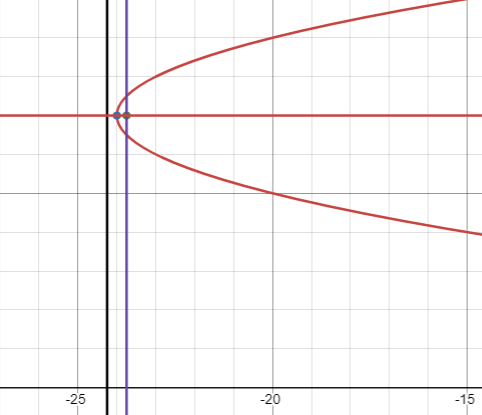
Problem 5 :
x = y2 - 14y + 25
Solution :
x = y2 - 14y + 25
x = y2 - 2 y (7) + 72 - 72 + 25
x = (y - 7)2 - 49 + 25
x = (y - 7)2 - 24
x + 24 = (y - 7)2
(y - 7)2 = x + 24
Comparing with (y - k)2 = 4a(x - h), we know that the parabola is symmetric about x axis and it opens rightward.
4a = 1
a = 1/4
|
Direction of opening |
Opening up |
|
Vertex |
(h, k) ==> (-24, 7) |
|
Focus |
h + a = -24 + (1/4) = -95/4 (h + a, k) ==> (-95/4, 7) |
|
Equation of latus rectum |
x = h + a x = -95/4 |
|
Equation of directrix |
x = h - a x = -24 - (1/4) x = -97/4 |
|
Equation of axis of symmetry |
y = k y = 7 |
|
Length of latus rectum |
4a = 1 unit |
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling