HOW TO FIND UNKNOWN ANGLES OF A RHOMBUS

What is rhombus ?

A rhombus is a quadrilateral in which all sides are equal is length.

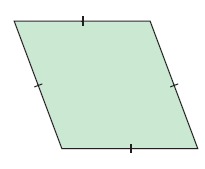
• Opposite angles are equal in size.
• Diagonals bisect each other at right angles.
• Diagonals bisect the angles at the vertex.

Problem 1 :

For rhombus JMLK, find each angle measure.

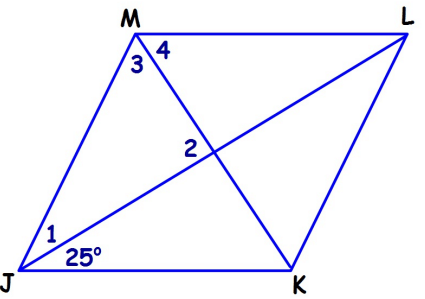
1)  ∠1      2)  ∠2      3)  ∠3     4)  ∠4      5)  ∠JML      6)  ∠MLK

Solution :

1)  ∠1  =  25 (Diagonals bisect the angles)

2)  ∠2  =  90

3)  ∠3 :

∠1 + ∠2  +∠3 = 180

25 + 90 + ∠3 = 180

115 + ∠3 = 180

∠3 = 180 -115

∠3 = 65

4)  ∠4 = 65

5)  ∠JML :

∠JML = ∠3 + ∠4

 = 65 + 65

= 130

6)  ∠MLK :

∠MJK = ∠MLK 

∠MLK = ∠1 + ∠2

 = 25 + 25

= 50

Problem 2 :

For rhombus JLMK, find each line segment and angle measure.

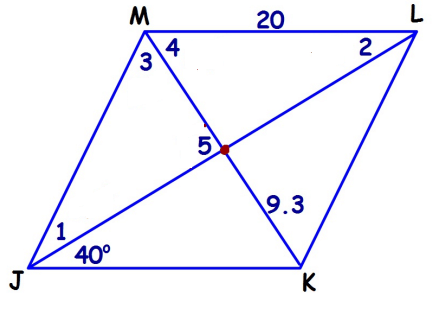
1)  ∠1      2)  ∠2      3)  ∠3     4)  ∠4      5)  ∠5      6)  LK    7)  MK

Solution :

1)  ∠1 = 40

2)  ∠2 = 40

3)  ∠3 :

∠1 + ∠5 + ∠3 = 180

40 + 90 + ∠3 = 180

130 + ∠3 = 180

∠3 = 180 - 130

∠3 = 50

4)  ∠4 = ∠3 = 50

5)  ∠5 = 90

6)  LK = 20

7)  MK = 9.3 + 9.3 ==> 18.6

Problem 3 :

For rhombus SLTM, find the missing values. If ∠1 = 3x + 8, ∠2 = 11x - 24, find

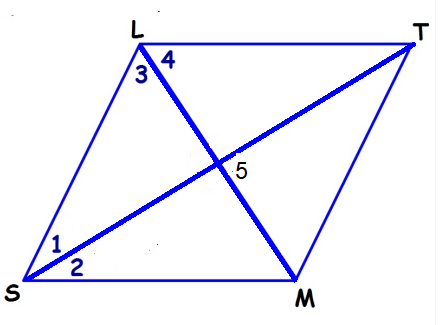
1)  x =      2)  ∠1      3)  ∠2     4)  ∠3      5)  ∠4      6)  ∠5

Solution :

Since the diagonal will bisect the angle,

∠1 = ∠2

3x + 8 = 11x - 24

3x - 11x = -24 - 8

-8x = -32

x = 32/8

x = 4

2)  ∠1 = 3x + 8

= 3(4) + 8

= 12 + 8

 ∠1  = 20

3)  ∠2 = 20

4)  ∠3  :

In the triangle,

The diagonals will intersect at right angle.

∠1 + ∠3 + 90 = 180

20 + ∠3 + 90 = 180

110 + ∠3 = 180

∠3 = 180 - 110

∠3 = 70

5)  ∠4  =  70

6)  ∠5 = 90

Problem 4 :

For rhombus SLTM, find the missing values, if ∠1 = 5x and ∠2 = x² - 50, find 

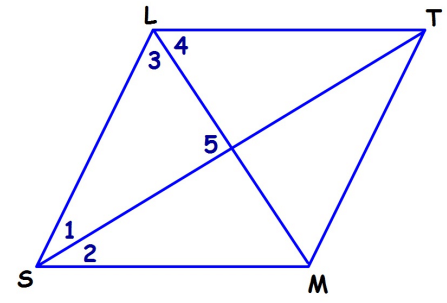
1)  x =      2)  ∠1      3)  ∠2     4)  ∠3      5)  ∠4      6)  ∠5

Solution :

∠1 = ∠2 (since the diagonal will bisect the angle at vertex)

5x = x² - 50

x² - 5x - 50 = 0

(x - 10) (x + 5) = 0

x = 10 and x = -5 (not admissible)

2)  ∠1 = 5x ==> 5(10) ==> 50

3)  ∠2 = 50

4)  ∠3 :

∠1 +  ∠3 +  ∠5 = 180

50 + ∠3 + 90 = 180

140 + ∠3 = 180

∠3 = 180 - 140

∠3 = 40

5)  ∠4 = 40

6)  ∠5 = 90

Problem 5 :

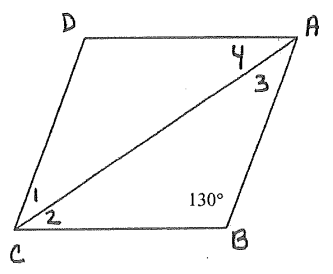
Find

1)  ∠D  2)  ∠DCB    3) ∠1    4)  ∠2     5)  ∠3      6)  ∠4

Solution :

1)  ∠D = 130 = ∠B

2)  ∠DCB = ∠1 + ∠2

In triangle ACB,

∠2 + ∠3 + ∠ABC = 180

∠2 = ∠3

∠2 + ∠2 + 130 = 180

2 ∠2 = 180 - 130

2 ∠2 = 50

∠2 = 50/2

∠2 = 25

∠1 = ∠2 (angle bisector)

∠DCB = 25 + 25

∠DCB = 50

3) ∠1 = ∠2 = ∠3 = ∠4 = 25

Problem 6 :

Find all missing angles.

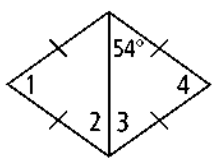
Solution :

The triangle, which is on the right

54 + ∠3 + ∠4 = 180

∠3 = 54

54 + 54 + ∠4 = 180

108 + ∠4 = 180

∠4 = 180 - 108

∠4 = 72

∠1 = 72

∠2 = 54

Problem 7 :

Find the measure of the numbered angles.

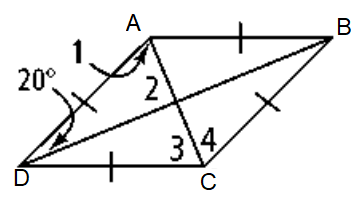
Solution :

In triangle ADB, 

∠ADB + ∠ABD + ∠DAB = 180

20 + 20 + ∠DAB = 180

∠DAB = 180 - 40

∠DAB = 140

∠1 = 140/2 ==> 70

20 + ∠1 + ∠2 = 180

20 + 70 + ∠2 = 180

∠2 = 180 - 90

∠2 = 90

∠3 = 70

∠4 = 70