HOW TO FIND THIRD DEGREE POLYNOMIAL FROM ZEROES

Problem 1 :

Find all third degree real polynomials with zeroes of -1/2 and 1-3i.

Solution :

Let the zeroes are p, q and r.

p = -1/2, q = 1 - 3i and r = 1 + 3i

From the complex roots, we can create a quadratic factor.

Sum of roots = 1 - 3i + 1 + 3i ==> 2

Product of roots = (1 - 3i)(1 + 3i)

= 1² - (3i)²

= 1 - 9(-1)

= 10

y = x² - 2x + 10

Another zero is x = -1/2

Converting into factor, we get

y = (x + 1/2)

Multiplying linear and binomial factor, we get

y = a (2x + 1)(x² - 2x + 10), where a ≠ 0

Problem 2 :

p(x) is a real cubic polynomial in which p(1) = p(2 + i) = 0 and p(0) = -20. Find p(x) in expanded form.

Solution :

p(1) = 0, p(2 + i) = 0

From this we understand two x-intercepts are 1 and 2 + i. Since one of the roots is  a complex number, its conjugate can be considered as another root.

Roots are x = 1, x = 2 + i and x = 2 - i

From the complex roots, creating quadratic factor, we get

Sum of roots = 2 + i + 2 - i ==> 4

Product of roots = (2 + i)(2 - i)

= 4 - i²

= 4 + 1

= 5

Quadratic factor :

y = x² - 4x + 5

Another zero is x = 1

Creating factor, we get

x - 1

Multiplying the factors, we get

y = a(x - 1)(x² - 4x + 5), where a ≠ 0

From the above information, it is clear the curve is passing through the point (0, -20).

-20 = a(0 - 1)(0² - 4(0) + 5)

-20 = -5a

a = 4

Applying the value, we get

y = 4(x - 1)(x² - 4x + 5)

Problem 3 :

5 - i is a zero of 2z³ + az² + 62z + (a - 5), where a is real. Find a and other two zeroes are.

Solution :

Since the given zero is complex number, then another zero will be its conjugate.

Quadratic factor :

= z² - (5 + i + 5 - i)z + (5² - i²)

= z² - 10z + 26

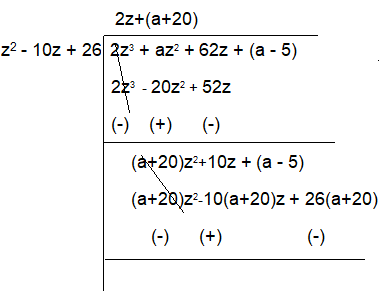
Quotient = 2z + (a + 20)

10 + 10(a + 20) = 0

10 + 10a + 200 = 0

210 + 10a = 0

10a = -210

a = -210/10

a = -21

The value of a is -21.

Applying the value of a in quotient, we get

= 2z + (-21 + 20)

= 2z + 1

Equating each factor to zero, we get

2z + 1 = 0

z = -1/2

Problem 4 :

-2/3 and 2 are zeroes of 6x³ + ax² - 4ax + b. Find the value of a and b.

Solution :

Zeroes are x = -2/3 and x = 2.

Let y = 6x³ + ax² - 4ax + b

When x = -2/3, y = 0

0 = 6(2)³ + a(2)² - 4a(2) + b

-48 = 4a -8a + b

-4a + b = -48 ----(2)

(1) + (2) x 7 ==> 

28a + 9b - 28a + 7b = 16 - 336

16b = -320

b = -20

Applying the value of b in (2), we get

-4a - 20 = -48

-4a = -28

a = 7