HOW TO FIND THE VOLUME OF SIMILAR SOLIDS

If the sides of a rectangular prism are multiplied by k, a similar prism is obtained.

The new volume = ka × kb × kc

= k³ abc

= k³ × old volume

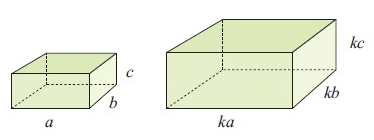
If a 3 – dimensional object is enlarged by a scale factor of k, then

The volume of the image = k³ × the volume of the object.

Problem 1 :

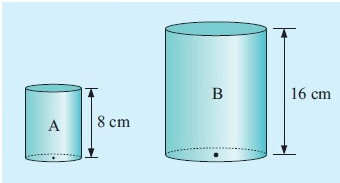
Two soup cans are similar and have heights of 8 cm and 16 cm respectively. Cylinder A has volume 225 cm³.

Find : a) the ratio of their radii.

b) the volume of B.

Solution :

a) When A is enlarged to give B,

k = 16/8 = 2

Therefore the ratio of radii = 1 : 2

b) Volume of  B = k³ × volume of A

= 2³ × 225 cm³

= 1800 cm³

The following contain similar solids. Find the unknown length or volume :

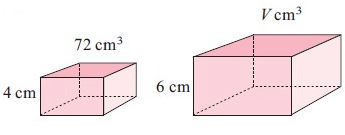
Problem 2 :

Solution :

6 = k × 4

k = 6/4

k = 3/2

Volume of new shape = k³ × volume of old shape

= (3/2)³ × 72

= 27/8 × 72

= 243

So, volume is 243 cm³. 

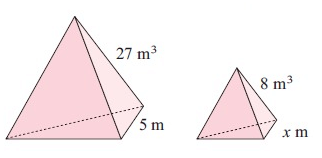
Problem 3 :

Solution :

large prism = k³ ⋅ small prism

27 = k³ × 8

k³ = 27/8

k = ∛(27/8)

k = 3/2

Length of larger = k ⋅ length of smaller

5 = 3/2 ⋅ x

5 × 2/3 = x

10/3 = x

3 1/3 = x

So, length is 3 1/3 m.

Problem 4 :

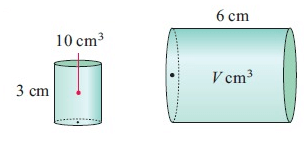
Solution :

6 = k × 3

k = 6/3

k = 2

Volume of new shape = k³ × volume of old shape

= k³ × 10

= (2)³ × 10

= 8 × 10

= 80

So, volume is 80 cm³.

Problem 5 :

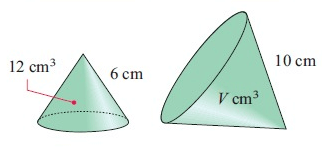
Solution :

10 = k × 6

k = 10/6

k = 5/3

Volume of new shape = k³ × volume of old shape

= (5/3)³ × 12

= 125/27 × 12

= 55.5

So, volume is 55.5 cm³.

Problem 6 :

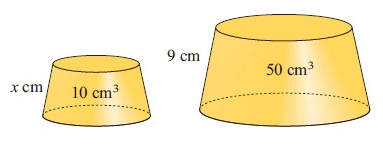
Solution :

50 = k³ × 10

k³ = 50/10

k³ = 5

k = ∛5

k = 1.710

Slant height of larger frustum cone = k × Slant height of smaller frustum cone

9 = 1.710 ⋅ x

9/1.710 = x

5.26 = x

So, length is 5.26 cm.

Problem 7 :

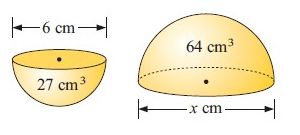
Solution :

64 = k³ × 27

k³ = 64/27

k = ∛(64/27)

k = 4/3

Diameter of larger hemisphere = k × diameter of smaller hemisphere

x = 4/3 × 6

x = 8

So, length is 8 cm.