HOW TO FIND THE RELATED ANGLE FROM THE PRINCIPAL ANGLE

Standard position :

The angle in the cartesian plane is standard position if its vertex lies at the origin and its initial arm lies on the positive axis.

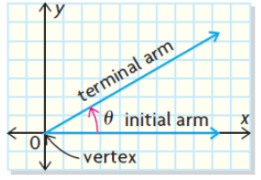
Principal Angle (θ) :

The counter-clockwise angle between the initial arm and the terminal arm of an angle in standard position. Its value is between 0° and 360°.

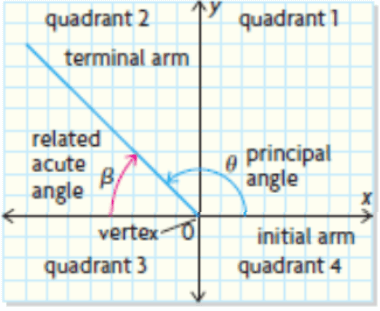
Related Acute Angle (β) :

The acute angle between the terminal arm of an angle in standard position and the x-axis when the terminal arm lies in quadrants 2, 3, or 4.

An angle in standard position is determined by a counterclockwise rotation and is always positive. An angle determined by a clockwise rotation is always negative.

Given Angle is Positive

If θ is positive but greater than 360°, find the positive angle between 0° and 360° that is coterminal with θ°.

To get the coterminal angle, divide θ by 360° and take the remainder.

Given Angle is Negative

If θ is negative, add multiples of 360° to θ make the angle as positive such that it is between 0° and 360°.

Once we have the given angle as positive and also it is between 0° and 360°, easily we can find the reference angle or related angle as explained below.

Principal angle 1st quadrant 2nd quadrant 3rd quadrant 4th quadrant

Related angle the same 180 - given angle given angle - 180 360 - given angle

State the related angle for the principal angle shown

Problem 1 :

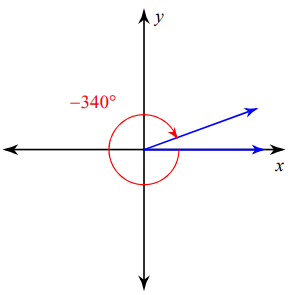
Solution :

Since the given angle is negative, to make it as positive we add 360.

= -340^º + 360^º

= 20^º

The terminal side is in the 1st quadrant. So, the same can be taken as related angle. Then, the required related angle for -340^º is 20^º.

Problem 2 :

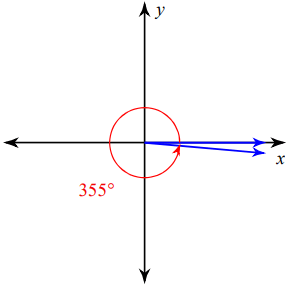
Solution :

The terminal side is on the 4th quadrant. 

Related angle = 360^º - 355^º

= 5^º

So, the required related angle for 355^º

^5º

Problem 3 :

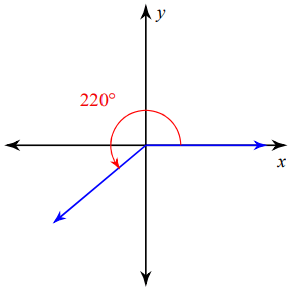
Solution :

The terminal side lies in 3rd quadrant, the formula given below can be used to find the related angle.

Related angle = given angle - 180

= 220 - 180

= 40^º

Problem 4 :

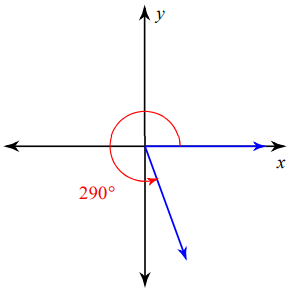
Solution :

The terminal side lies in 4th quadrant, the formula given below can be used to find the related angle.

Related angle = 360 - given angle

= 360 - 290

= 70^º

Problem 5 :

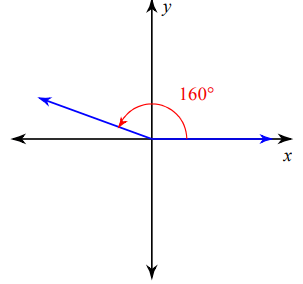
Solution :

The terminal side lies in 2nd quadrant, the formula given below can be used to find the related angle.

Related angle = 180 - given angle

= 180 - 160

= 20^º

Problem 6 :

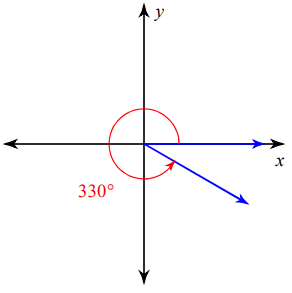
Solution :

The terminal side lies in 4th quadrant, the formula given below can be used to find the related angle.

Related angle = 360 - given angle

= 360 - 330

= 30^º