HOW TO FIND THE PERIOD AND AMPLITUDE OF SINE AND COS FROM GRAPH

A periodic function is one which repeats itself over and over in horizontal direction.

What is period ?

The period of a periodic function is the length of one repetition or cycle

What is amplitude ?

The amplitude is the vertical distance between a maximum point and the principal axis.

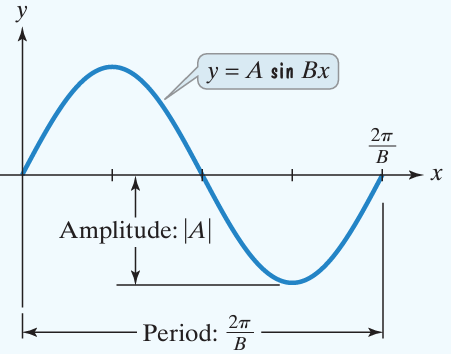
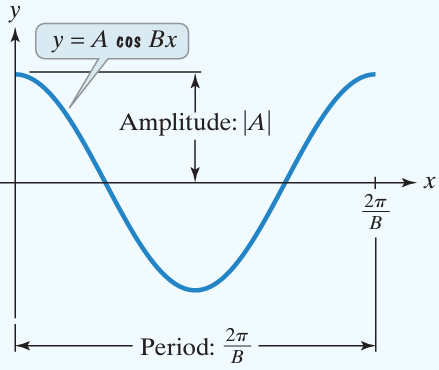
• The amplitude is |A|
• Period is 2π/B, for B > 0

Give the amplitude and period of each function graphed below. Then write an equation of each graph.

i) Amplitude

ii) Period

iii) Equation

Problem 1 :

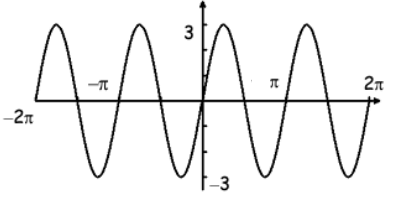
Solution :

i) By observing the pattern, it is the graph of sine function. Every sin functions will be in the form y = A sin Bx

Midline is x = 0, maximum = 3 and minimum = -3

Amplitude = (max - min)/2

= (3 - (-3))/2

= (3 + 3)/2

= 6/2

= 3

ii)  Horizontal length of one cycle = π

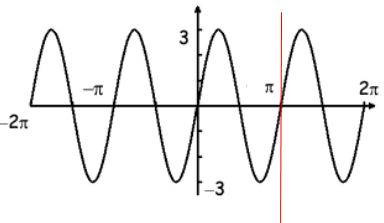
Period = 2π/|B|

π = 2π/|B|

|B| = 2π/π

B = 2

iii) So, the equation represented by the graph is 

y = 3 sin 2x

Problem 2 :

Solution :

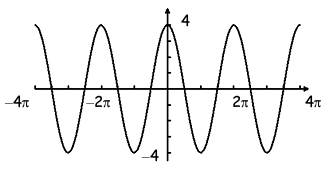
i) By observing the pattern, it is the graph of cosine function. Every cosine functions will be in the form y = A cos Bx

Midline is x = 0, maximum = 4 and minimum = -4

Amplitude = (max - min)/2

= (4 - (-4))/2

= (4 + 4)/2

= 8/2

= 4

ii)  Horizontal length of one cycle = 2π

Period = 2π/|B|

2π = 2π/|B|

|B| = 2π/2π

B = 1

iii) So, the equation represented by the graph is 

y = 4 cos x

Problem 3 :

Solution :

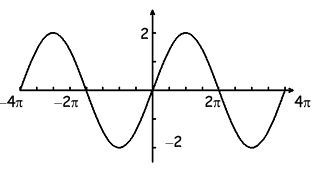
i) By observing the pattern, it is the graph of sin function. Then, the required function will be in the form y = A sin Bx

Midline is x = 0, maximum = 2 and minimum = -2

Amplitude = (max - min)/2

= (2 - (-2))/2

= (2 + 2)/2

= 4/2

= 2

ii)  Horizontal length of one cycle = 4π

Period = 2π/|B|

4π = 2π/|B|

|B| = 2π/4π

B = 1/2

iii) So, the equation represented by the graph is 

y = 2 sin (1/2)x

Problem 4 :

Solution :

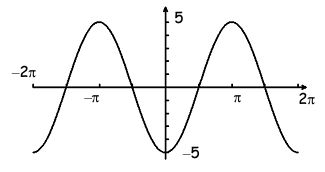
i) By observing the graph look like a reflection of cosine function. Then, the required function will be in the form

y = A cos Bx

Midline is x = 0, maximum = 5 and minimum = -5

Amplitude = (max - min)/2

= (5 - (-5))/2

= (5 + 5)/2

= 10/2

= 5

ii)  Horizontal length of one cycle = 2π

Period = 2π/|B|

2π = 2π/|B|

|B| = 2π/2π

B = 1

iii) So, the equation represented by the graph is 

y = -5 cos x

Problem 5 :

Solution :

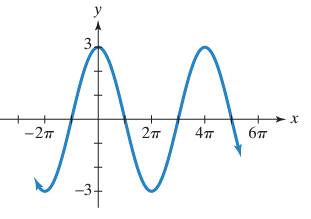
i) By observing the graph look like a reflection of cosine function. Then, the required function will be in the form

y = A cos Bx

Midline is x = 0, amplitude = 3

ii)  Horizontal length of one cycle = 4π

Period = 2π/|B|

4π = 2π/|B|

|B| = 2π/4π

B = 1/2

iii) So, the equation represented by the graph is 

y = 3 cos (1/2) x

Problem 6 :

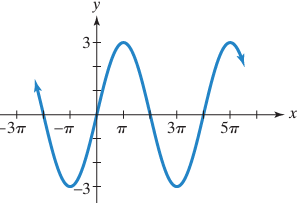
Solution :

i) By observing the graph looks like a graph of sin function. Then, the required function will be in the form

y = A sin Bx

Midline is x = 0, amplitude = 3

ii)  Horizontal length of one cycle = 4π

Period = 2π/|B|

4π = 2π/|B|

|B| = 2π/4π

B = 1/2

iii) So, the equation represented by the graph is 

y = 3 sin (1/2) x

Problem 7 :

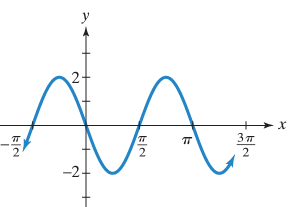
Solution :

i) By observing the graph look like a reflection of sin function. Then, the required function will be in the form

y = A sin Bx

Midline is x = 0, amplitude = 2

ii)  Horizontal length of one cycle = π

Period = 2π/|B|

π = 2π/|B|

|B| = 2π/π

B = 2

iii) So, the equation represented by the graph is 

y = -2 sin 2 x