HOW TO FIND THE LONGEST SIDES OF A TRIANGLE GIVEN ANGLES

The following triangles are not drawn to scale.

(i) Find the missing angle

(ii)  State the longest side of each triangle.

Problem 1 :

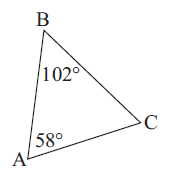
Solution :

(i)  ∠A = 58°, ∠B = 102°, ∠C = ?

Sum of interior angles of a triangle = 180°

∠A + ∠B + ∠C = 180°

58 + 102 + ∠C = 180°

160 + ∠C = 180°

∠C = 180° - 160

∠C = 20°

(ii)  The side which is opposite to the largest angle measure is AC.

So, AC is the largest side.

Problem 2 :

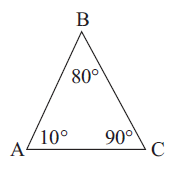
Solution :

In this triangle, we know each angle measure and it is right triangle.

The largest angle measure is ∠C. The side which is opposite this angle measure is AB.

So, the longest side of the given triangle is AB.

Problem 3 :

List the sides of each triangle in order from shortest to longest.

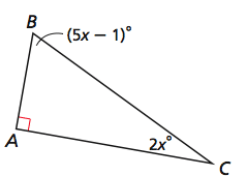
Solution :

∠A + ∠B + ∠C = 180

∠A = 90, ∠B = 5x - 1 and ∠C = 2x

90 + 5x - 1 + 2x = 180

7x + 89 = 180

Subtracting 89 on both sides.

7x = 180 - 89

7x = 91

Divide by 7 on both sides.

x = 91/7

x = 13

∠A = 90, ∠B = 64 and ∠C = 26

Ordering from least to greatest.

AB < AC < BC

Problem 4 :

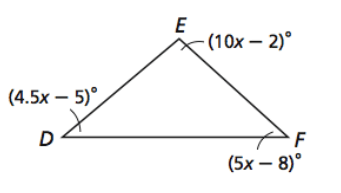
Solution :

∠D = 4.5x - 5,∠E = 5x - 8 and ∠F = 10x - 2

∠D + ∠E + ∠F = 180

4.5x - 5 + 5x - 8 + 10x - 2 = 180

19.5x - 13 - 2 = 180

19.5x - 15 = 180

Add 15 on both sides.

19.5x = 180 + 15

19.5x = 195

Dividing by 19.5 on both sides.

x = 195/19.5

x = 10 

Ordering sides from least to greatest.

EF < DE < DF

Problem 5 :

Determine the Longest side of ∆MNO, where m∠M = 56, m∠N = 108, and m∠O = 16

Solution :

Greatest angle measure = 108, greatest side = MO

Smallest angle = 16, smallest side = MN

Problem 6 :

List the sides in order from shortest to longest in ∆ XYZ :

with m∠X = 50, m∠Y = 5x + 10 and m∠Z = 5x.

Solution :

m∠X + m∠Y + m∠Z = 180

50 + 5x + 10 + 5x = 180

10x + 60 = 180

Subtracting 60 on both sides.

10x = 180 - 60

10x = 120

Dividing by 10 on both sides.

x = 120/10

x = 12

Ordering from least to greatest.

YZ < XY < ZX.

Problem 7 :

Which is the longest and which is the smallest.

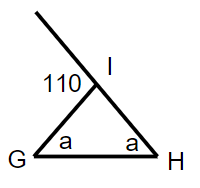
Solution :

Accordingly exterior angle theorem,

m∠G + m∠H = m∠I 

a + a = 110

2a = 110

Dividing by 2

a = 110/2

a = 55

So, the longest side is GH. Smallest side GI = HI

Problem 8 :

Which is the longest and which is the smallest.

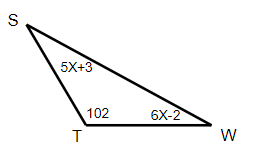
Solution :

m∠S = 5x + 3, m∠T = 102, m∠W = 6x - 2

m∠S + m∠T + m∠W = 180

5x + 3 + 102 + 6x - 2 = 180

11x + 105 - 2 = 180

11x + 103 = 180

Subtracting 103 on both sides.

11x = 180 - 103

11x = 77

Dividing by 11 on both sides.

x = 77/11

x = 7

Smallest side = TW, longest side = SW.

Problem 9 :

Find the longest side.

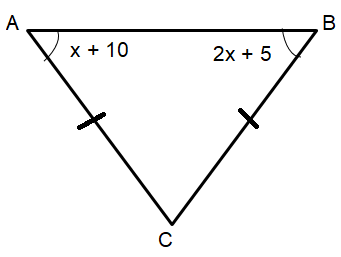
Solution :

m∠A = m∠B

x + 10 = 2x + 5

2x - x = 10 - 5

x = 5

m∠A + m∠B + m∠C = 180

15 + 15 + m∠C = 180

m∠C = 180 - 30

m∠C = 150

So, the longest side is AB.