HOW TO FIND THE LENGTH OF A LINE SEGMENT WITH COORDINATES

To find the distance between two points, we will use the formula given below.

Distance between two points = length of the line segment

The endpoints can be considered as the following.

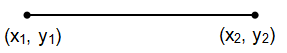
Calculate the length of the line joining the points A and B.

Problem 1 :

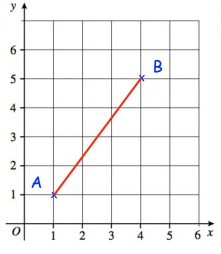
Solution:

Given, A(1, 1) and B(4, 5)

Problem 2 :

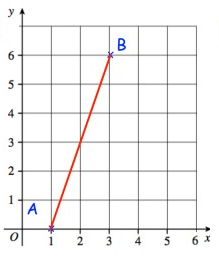
Solution:

Given, A(1, 0) and B(3, 6)

Problem 3 :

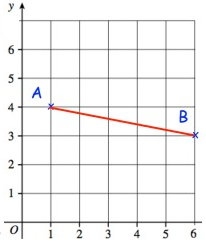
Solution:

Given, A(1, 4) and B(6, 3)

Calculate the length of the line joining the point A and B.

Problem 4 :

Solution:

Given, A(7, 12) and B(12, 0)

Problem 5 :

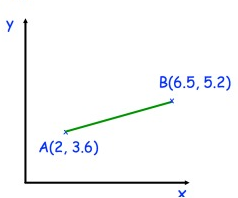
Solution:

Given, A(2, 3.6) and B(6.5, 5.2)

Problem 6 :

Calculate the perimeter of triangle ABC.

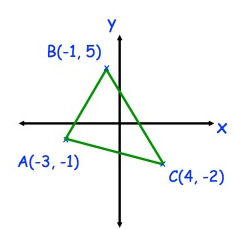
Solution:

Perimeter = AB + BC + AC

= 2√10 + √74 + 5√2

Problem 7 :

The distance between the points (1, 2) and (16, p) is 17. Find the possible values of p.

Solution:

Problem 8 :

The distance between the points (-3, -4) and (q, 5) is 15. Find the possible values of q.

Solution: