HOW TO FIND THE LEAST NUMBER TO BE SUBTRACTED TO GET A PERFECT SQUARE

Problem 1 :

What is the smallest number to be subtracted from 549162 in order to make it a perfect square?

a)   28     b)   36     c)   62     d)   81

Solution :

Put comma for every two digits starting from the last.

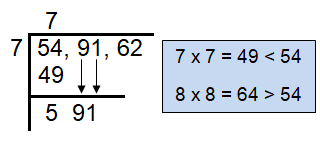
To get the next step, we will multiply the quotient by 2.

Now multiply 74 by 2, we get 148.

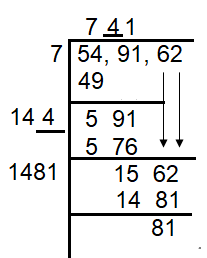
The nearest perfect square (741)²

(741)² = 549081

549081 < 549162

To get the number to be subtracted = 549162 - 549081

= 81

So option (d) is correct.

Problem 2 :

What is the least number which should be subtracted from 0.000326 to make it a perfect square?

a)   0.000002   b)   0.000004    c)   0.02    d)   0.04

Solution :

The given number is 0.000326 = 326 × 10^-6

= (324 + 2) × 10^-6

= (18 × 18 + 2) × 10^-6

326 - 2 is a square number.

Therefore, 2 × 10^-6  = 0.000002 should be subtracted from 0.000326.

So, option (a) is correct.

Problem 3 :

A general wishes to draw up his 36581 soldiers in the form of a solid square. After arranging them, he found that some of them are left over. How many are left ?

(a)  65     (b) 81   (c)  100   (d) None

Solution :

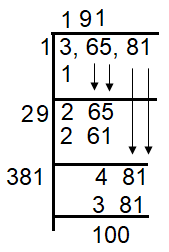
So, 100 is the left over.

Problem 4 :

Find the smallest number that must be subtracted to 1780 to make it a perfect square.

Solution :

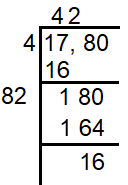
(42)² = 1764

1764 < 1780

So, the required number to be subtracted is 16.

Problem 5 :

Find the least number which must be subtracted from 3250 so as to get a perfect square

Solution :

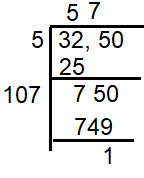
So, 1 to be subtracted to make 3250 as perfect square.