HOW TO FIND THE EXACT VALUE OF A TRIG FUNCTION

Example 1 :

Find the exact value of cos (7π/4)

Solution :

Converting radian to degree 

7π/4 = (7π/4) x (180/π)

= 315

The required angle lies in 4^th quadrant. Reference angle = 360 - 315 ==> 45 degree

cos (315) = cos 45

Note :

In 4th quadrant, for the trigonometric ratios cos θ and its reciprocal sec θ only will have positive sign.

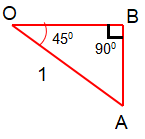
cos θ = Adjacent side / Hypotenuse

cos θ = OB/OA

AB = OB

OA = √2(OB)

1 = √2(OB)

1/√2 = OB

cos (7π/4) = cos 315  = cos 45

= (1/√2) / 1

cos (7π/4) = 1/√2

Example 2 :

Find the exact value of sin (-30°)

Solution :

sin (-30°) = - sin 30°

Angle lies in 1^st quadrant.

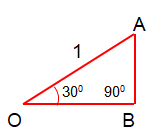
sin θ = Opposite side / Hypotenuse

sin θ = AB/OA

OA = 2(AB)

1/2 = AB

-sin 30° = (-1/2)/1

-sin 30° = -1/2

Example 3 :

Find the exact value of cos (600°)

Solution :

cos 600° = cos (360 + 240°)

cos 600° = cos 240°

Angle lies in 3^rd quadrant. Refence angle = 240-180 ==> 60

Note :

In 3rd quadrant, for the trigonometric ratios tan θ and its reciprocal cot θ only will have positive sign.

cos 240° = -cos 60°

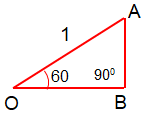
cos θ = Adjacent side / Hypotenuse

cos θ = OB/OA

OA = 2(OB)

1 = 2OB

OB = 1/2

-cos 60° = (-1/2)/1

cos 240°  = -cos 60° = -1/2

Example 4 :

Find the exact value of sin (9π/2)

Solution :

Converting radian to degree 

9π/2 = (9π/2) x (180/π)

= 810

sin 810° = sin (2 x 360 + 90°)

sin 810° = sin 90°

= 1

Example 5 :

Find the exact value of tan (585°)

Solution :

tan 585° = cos (360 + 225°)

tan 585° = tan 225°

Angle lies in 3^rd quadrant. Refence angle = 270 - 225 ==> 45

Note :

In 3rd quadrant, for the trigonometric ratios tan θ and its reciprocal cot θ only will have positive sign.

tan 225° = tan 45°

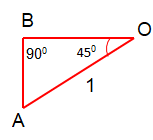
tan θ = Opposite side / Adjacent side

tan θ = OB/AB

OA = √2(AB)

1/√2 = AB = OB

tan 45° = (1/√2) / (1/√2)

tan 45° = 1

Example 6 :

Find the exact value of cos (23π/6)

Solution :

Converting radian to degree 

23π/6 = (23π/6) x (180/π)

= 690

cos 690° = cos (360 + 330°)

cos 690° = cos 330°

Angle lies in 4^th quadrant. Refence angle = 360 - 330 ==> 30

Note :

In 4th quadrant, for the trigonometric ratios cos θ and its reciprocal sec θ only will have positive sign.

cos 690° = cos 330° = cos 30°

= √3/2

Example 7 :

Find the exact value of cos (-11π/4)

Solution :

cos (-11π/4) = cos (11π/4)

Converting radian to degree 

11π/4 = (11π/4) x (180/π)

= 495

cos 495° = cos (360 + 135°)

cos 495° = cos 135°

Angle lies in 2^nd quadrant. Refence angle = 180 - 135 ==> 45

Note :

In 2nd quadrant, for the trigonometric ratios sin θ and its reciprocal cosec θ only will have positive sign.

cos 495° = cos 135° = -cos 45°

= -√2/2 (or) -1/√2

Example 8 :

Find the exact value of sin (-13π/4)

Solution :

sin (-13π/4) = -sin (13π/4)

Converting radian to degree 

13π/4 = (13π/4) x (180/π)

= 585

sin 585° = -sin (360 + 225°)

sin 585° = -sin 225°

Angle lies in 3^rd quadrant. Refence angle = 225 - 180 ==> 45

Note :

In 3rd quadrant, for the trigonometric ratios tan θ and its reciprocal cot θ only will have positive sign.

sin 225° = -(-sin 45°)

= √2/2 (or) 1/√2