HOW TO FIND THE EQUATION OF A CUBIC FUNCTION FROM A GRAPH

All cubic are continuous smooth curves. Every cubic polynomials must cut the x-axis at least once and so at least one real zero.

Cubic Equation with Three Distinct Roots

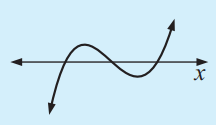
For a cubic of the form

p(x) = a (x - p)(x - q)(x - r)

the graph has three distinct x-intercepts corresponding to the three real. The distinct zeroes are p, q and r.

Cubic Equation with Repeated Roots

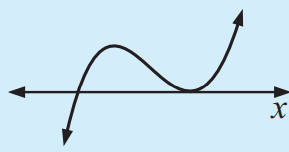
For a cubic of a form 

p(x) = a (x - p)²(x - q)

the graph touches the x-axis at the repeated zero p and cuts it at the other x-intercept q as shown.

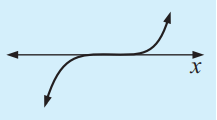
For a cubic of a form

p(x) = a (x - p)³ 

the graph touches the x-axis at p. The graph is horizontal at this point and the x-axis is a tangent to the curve, even though the curve crosses over it.

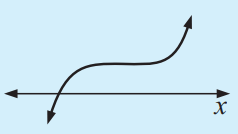
Cubic Equation with No Real Roots

For a cubic of the form

p(x) = a(x - p) (ax² + bx + c)

where Δ < 0, there is only one x-intercept p. The graph cuts the x-axis at this point. The other two zeroes are imaginary and so do not show up on the graph.

Find the equation of the cubic with the graph.

Problem 1 :

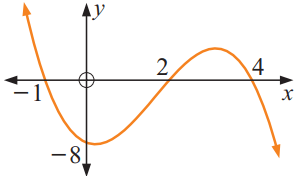
Solution :

x - intercepts :

x = -1, x = 2 and x = 4

Converting into factors, we get

(x + 1) (x - 2) (x - 4)

The required cubic function will be

y = a (x + 1) (x - 2) (x - 4)

We observe that the curve is passing through the point (0, -8).

-8 = a(0 + 1) (0 - 2) (0 - 4)

-8 = a(1)(-2)(-4)

-8 = a(8)

a = -1

y = -1 (x + 1) (x - 2) (x - 4)

Converting into standard form,

y = -1(x + 1)(x² - 6x + 8)

y = -1(x³ - 6x² + 8x + x² - 6x + 8)

y = -1(x³ - 5x² + 2x + 8)

y = -1x³ + 5x² - 2x - 8

Problem 2 :

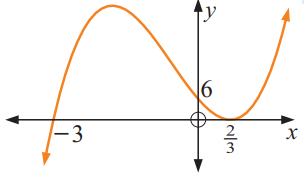
Solution :

x - intercepts :

At -3, the curve crosses the x axis, at 2/3 the curve touches the x-axis. So, we have repeated factors.

x = -3, x = 2/3 and x = 2/3

Converting into factors, we get

(x + 3) (x - 2/3) (x - 2/3)

The required cubic function will be

We observe that the curve is passing through the point (0, 6).