HOW TO FIND THE DIMENSIONS OF A MATRIX WHEN MULTIPLYING
Determine whether each matrix product is defined. If so, state the dimensions of the product.
A2 × 5 and B5 × 4

The inner dimensions are equal so the matrix product is defined. The dimensions of the product are 2 × 4.
A1 × 3 and B4 × 3
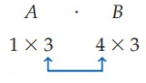
The inner dimensions are not equal, so the matrix product is not defined.
Determine whether each matrix product is defined. If so, state the dimensions of the product.
Problem 1 :
A3 × 5 · B5 × 2
Solution:
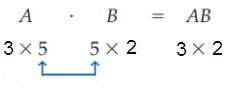
The inner dimensions are equal so the matrix product is defined. The dimensions of the product are 3 × 2.
Problem 2 :

Solution:
The inner dimensions are not equal, so the matrix product is not defined.
Find each product, if possible.
Problem 3 :
Solution:
- Dimension of the first matrix = 1 x 2
- Dimension of the second matrix = 2 x 2
- Then the result matrix will have the dimension of 1 x 2.
Problem 4 :
Solution:
- Dimension of the first matrix = 2 x 1
- Dimension of the second matrix = 1 x 3
- Then the result matrix will have the dimension of 2 x 3.
Problem 5 :
Solution:
- The dimension of the first matrix is 2 x 3
- The dimension of the second matrix is 2 x 2
Since the number of columns and number of rows in the matrices are not same, the product cannot be found. So, it is not possible.
Problem 6 :
Solution:
- Dimension of the first matrix = 2 x 2
- Dimension of the second matrix = 2 x 1
- Then the result matrix will have the dimension of 2 x 1
Determine whether each matrix product is defined. If so, state the dimensions of the product.
Problem 7 :
A4 × 3 ⋅ B3 × 2
Solution:
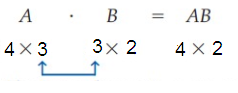
The inner dimensions are equal so the matrix product is defined. The dimensions of the product are 4 × 2.
Problem 8 :
X2 × 2 ⋅ Y2 × 2
Solution:
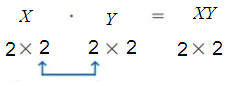
The inner dimensions are equal so the matrix product is defined. The dimensions of the product are 2 × 2.
Problem 9 :
P1 × 3 ⋅ Q4 × 1
Solution:
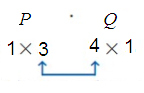
The inner dimensions are not equal, so the matrix product is not defined.
Problem 10 :
R1 × 4 ⋅ S4 × 5
Solution:
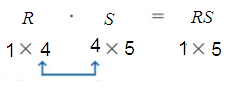
The inner dimensions are equal so the matrix product is defined. The dimensions of the product are 1 × 5.
Problem 11 :
M4 × 3 ⋅ S4 × 3
Solution:
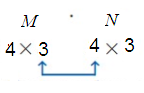
The inner dimensions are not equal, so the matrix product is not defined.
Problem 12 :
A3 × 1 ⋅ B1 × 5
Solution:
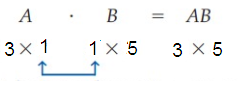
The inner dimensions are equal so the matrix product is defined. The dimensions of the product are 3 × 5.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling