HOW TO FIND THE ANGLES OF A PARALLELOGRAM

Find the measures of the indicated angles in each parallelogram.

Problem 1 :

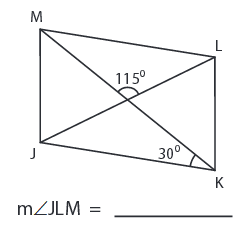
Solution :

The sum of the interior angles of a triangle is 180°.

∠KML = ∠MKJ = 30°

∠KML + ∠JLM + 115° = 180°

∠JLM  + 30° + 115° = 180°

∠JLM = 180° - 115° - 30°

∠JLM = 35°

Problem 2 :

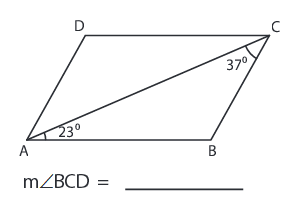
Solution :

DC II AB

 ∠DCA = ∠BAC = 23°

∠BCD = ∠ACB + ∠DCA

∠BCD = 23° + 37°

∠BCD = 60°

Problem 3 :

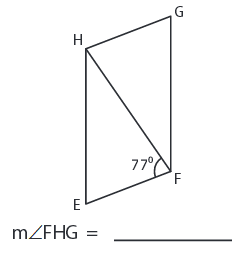
Solution :

The opposite angles are equal in a parallelogram.

∠FHG = ∠HFE = 77°

So, ∠FHG = 77°

Problem 4 :

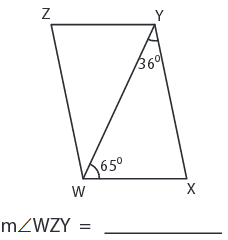
Solution :

The opposite angles are equal in a parallelogram.

∠WZY = ∠WXY

The sum of the interior angles of a triangle is 180°.

∠WXY = 180° - ∠XWY - ∠WYX

∠WZY = = 180° - 65° - 36°

∠WZY = = 79°

∠WZY = 79°

Problem 5:

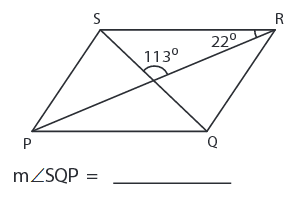
Solution :

The sum of the interior angles of a triangle is 180°.

∠SQP = 180° - (113 + 22)

∠SQP = 180° - 135°

∠SQP = 45°

Problem 6:

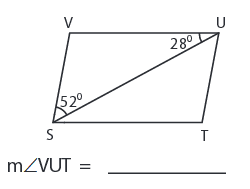
Solution :

∠VUT = ∠SUV + ∠SUT

∠VUT = 28° + 52°

∠VUT = 80°

Problem 6 :

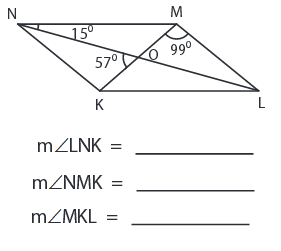
Solution :

In MNKL, ML II NK

So, ∠LNK = ∠NLM

∠MOL = ∠KON = 57° (vertical angles are equal)

∠LNK = 180° - ∠OML - ∠MOL

∠LNK = 180° - 99° - 57°

∠LNK = 24°

In ∆OMN,

∠NOK = ∠LNM + ∠OMN

∠OMN = ∠NOK - ∠LNM

∠OMN = 57° - 15°

∠OMN = 42°

The outside angle of a triangle is equal to the sum of two interior angles that are not adjacent to it.

NM II KL,

So, ∠MKL = ∠NMK = 42°

Problem 7 :

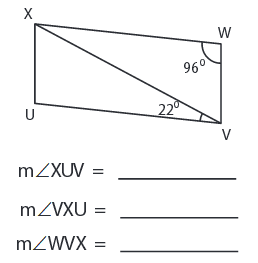
Solution :

∠XUV = ∠XWV = 96°

∠VXU = 180° - ∠XWV - ∠XVU

∠VXU = 180° - 96° - 22°

∠VXU = 62°

∠WVX = ∠VXU = 62°

Problem 8 :

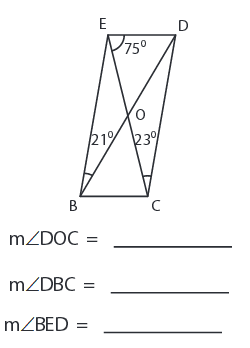
Solution :

BE II DC,

∠EBD = ∠BDC = 21°

∠DOC = 180° - (∠BDC + ∠DCE)

∠DOC = 180° - (21 + 23)

∠DOC = 180° - 44°

∠DOC = 136°

ED II BC,

∠DEC = ∠ECB = 75°

∠DBC = ∠DOC - ∠ECB

∠DBC = 136° - 75°

∠DBC = 61°

∠ECD = ∠BEC = 23°

∠BED = ∠BEC + ∠DEC

∠BED = 23° + 75°

∠BED = 98°