HOW TO FIND RELATIVE MAXIMUM AND MINIMUM FROM DERIVATIVE GRAPH

Problem 1 :

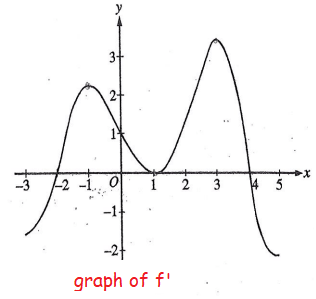
The graph of the derivative of a function f is shown in the figure above. The graph has horizontal tangent lines at x = -1, x = 1 and x = 3. At which of the following values of x does f have relative maximum ?

A)  -2 only     B)  1 only     C)  4 only   D) -1 and 3 only

E)  -2, 1 and 4.

Solution :

From the graph f'(x), x-intercepts of derivative functions are critical numbers of the original function f(x).

Analyzing the graph of f'(x) :

• Before -2, the curve is below the x-axis. So, in the interval (-∞, -2) f(x) will be decreasing then f(x) will have negative slope.
• After -2 upto 4, the curve is above the x-axis. So, in the interval (-2, 4) f(x) will be increasing then f(x) will have positive slope.
• After 4, the curve is below the x-axis. So, in the interval (4, ∞) f(x) will be decreasing then f(x) will have negative slope.

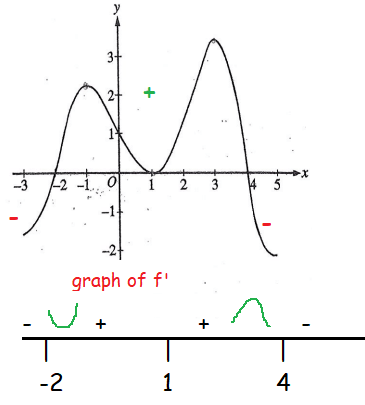
So, maximum value is at x = 4. Option C is correct.

Problem 2 :

The graph of f', the derivative of the function f is shown above for -3  ≤ x  ≤ 3. On what intervals is f increasing ?

A)  [-3, -1] only     B)  [-1, 3]        C)  [-2, 0] and [2, 3]

D)  [-3, -1] and [1, 3]

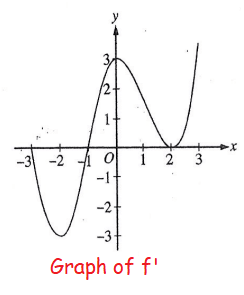
Solution :

x-intercepts of f'(x) = critical numbers of f(x)

Critical numbers of f(x) :

-3, -1 and 2

Analyzing the graph of f'(x) :

• In between -3 to -1, the curve is below the x-axis. So, in the interval (-3, -1) the function f(x) will be decreasing and f(x) will have negative slope.
• In between -1 and 3, the the curve is above the x-axis. So, in the interval (-1, 3) the function f(x) will be increasing and f(x) will have positive slope.

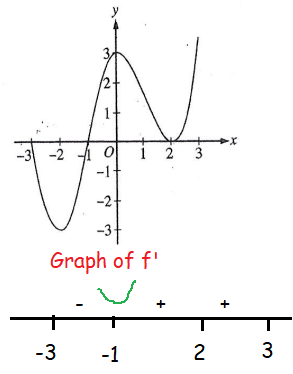
In the interval [-1, 3], the function is increasing.

Problem 3 :

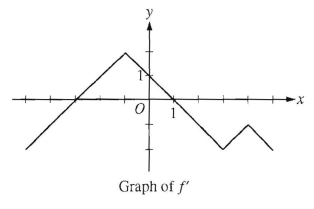
The graph of f', the derivative of f is shown above. The function f has local maximum at x = ?

A)  -3         B)  -1         C)  1         D)  3        E) 4

Solution :

f'(x) = 0, when x = -3 and x = 1

• These are critical points, to the left of -3, the graph is below the x-axis. So, it is decreasing.
• After -3 upto 1 it is above the x-axis. So, it is increasing.
• After 1, it is below the x-axis. So, it is decreasing.

Decreasing --> increasing --> decreasing

The, local maximum is at x = 1.

Problem 4 :

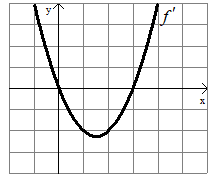
The graph of the derivative, f' of a function  f  is shown.

(a) On what interval(s) is  f  increasing or decreasing?  Justify your answer.

(b) At what value(s) of  x  does f  have a local maximum or local minimum?  Justify your answer.

Solution :

x-intercepts of the derivative function shown above are 0 and 3. These two are critical numbers of f(x).

• In the interval (-∞, 0), f'(x) is above the x-axis. So, the function f(x) will have positive slope. Increasing function in the interval (-∞, 0).
• In the interval (0, 3), f'(x) is below the x-axis. So, the function f(x) will have negative slope. Decreasing function in the interval (0, 3).
• In the interval (3, ∞), f'(x) is above the x-axis. So, the function f(x) will have positive slope. Increasing function in the interval (3, ∞).                

Increasing function ----> Decreasing function

At x = 0, the function f(x) has relative maximum.

Decreasing function ----> Increasing function

At x = 3, the function f(x) has relative minimum.

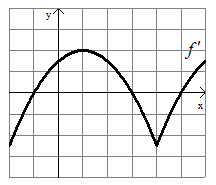
Problem 8 :

Solution :

x-intercepts of the derivative function shown above are -1, 3 and 5. These are critical numbers of f(x).

• In the interval (-∞, -1), f'(x) is below the x-axis. So, the function f(x) will have negative slope. Decreasing function in the interval (-∞, -1).
• In the interval (-1, 3), f'(x) is above the x-axis. So, the function f(x) will have positive slope. Increasing function in the interval (-1, 3).
• In the interval (3, 5), f'(x) is below the x-axis. So, the function f(x) will have negative slope. Decreasing  function in the interval (3, 5).
• In the interval (5, ∞), f'(x) is above the x-axis. So, the function f(x) will have positive slope. Increasing  function in the interval (5, ∞).

Decreasing ----> Increasing

At x = -1 and 5, the function f(x) has relative minimum.

Increasing ----> Decreasing

At x = 3, the function f(x) has relative maximum.