HOW TO FIND REAL ZEROES USING SYNTHETIC DIVISION

Problem 1 :

Use synthetic division to divide

f(x) = x³ + 12x² + 41x + 30 by x + 5.

Use the result to find all zeros of f.

A) (-5, 6, 1)     B) (5, -6, -1)     C) (-5, -6, -1)     D) (5, 6, 1)

Solution :

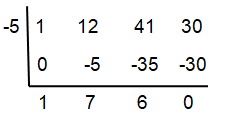
(x + 5) (x² + 7x + 6) = 0

(x + 5) (x + 6) (x + 1) = 0

x + 5 = 0, x + 6 = 0, x + 1 = 0

x = -5, x = -6, x = -1

So, option (C) is correct.

Problem 2 :

Use synthetic division to divide

f(x) = x³ + 1x² - 26x + 24 by x + 6

Use the result to find all zeros of f.

A) (-6, -4, -1)     B) (6, 4, 1)     C) (-6, 4, 1)     D) (6, -4, -1)

Solution :

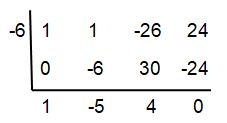
(x + 6) (x² - 5x + 4) = 0

(x + 6) (x - 4) (x - 1) = 0

x + 6 = 0, x - 4 = 0, x - 1 = 0

x = -6, x = 4, x = 1

So, option (C) is correct.

Problem 3 :

Use synthetic division to divide

f(x) = x³ - x² - 26x - 24 by x + 1.

Use the result to find all zeros of f.

A) (1, -6, 4)     B) (1, 6, -4)     C) (-1, -6, 4)     D) (-1, 6, -4)

Solution :

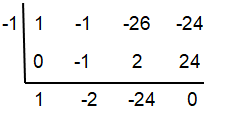
(x + 1) (x² - 2x - 24) = 0

(x + 1) (x - 6) (x + 4) = 0

x + 1 = 0, x - 6 = 0, x + 4 = 0

x = -1, x = 6, x = -4

So, option (D) is correct.

Use synthetic division to show that the number given to the right of the equation is a solution of the equation, then solve the polynomial equation.

Problem 4 :

x³ - 5x² + 2x + 8 = 0; 2

A) (4, 1, 2)     B) (-4, 1, 2)     C) (4, -1, 2)    D) (-4, -1, 2)

Solution :

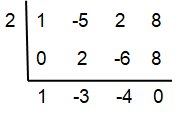
(x² - 3x - 4) (x - 2) = 0

(x - 4) (x + 1) (x - 2) = 0

x - 4 = 0, x + 1 = 0, x - 2 = 0

x = 4, x = -1, x = 2

So, option (C) is correct.

Problem 5 :

2x³ + 10x² - 4x - 48 = 0; -3

A) (2, -4, -3)     B) (-2, 4, -3)     C) (-2, -4, -3)     D) (2, 4, -3)

Solution :

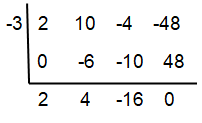
(2x² + 4x - 16) (x + 3) = 0

2(x² + 2x - 8) (x + 3) = 0

2(x - 2) (x + 4) (x + 3) = 0

x - 2 = 0, x + 4 = 0, x + 3 = 0

x = 2, x = -4, x = -3

So, option (A) is correct.