HOW TO FIND NUMBER OF SIDES OF POLYGON WITH ONE INTERIOR ANGLE

Problem 1 :

Each interior angle of a regular polygon is 174⁰. Find the number of sides of polygon.

Solution :

So, the number of sides of polygon is 6. Then the polygon is known as hexagon.

Problem 2 :

The interior angle of a regular polygon is 135⁰. Work out the number of sides of the polygon.

Solution :

So, the number of sides of the regular polygon is 8.

Problem 3 :

The sum of the interior angles in a polygon is 7380⁰. Calculate the number of sides the polygon has.

Solution :

Sum of the interior angles of a polygon = (n - 2) x 180

(n - 2) x 180 = 7380

n - 2 = 7380/180

n - 2 = 41

Add 2 on both sides, we get

n = 41 + 2

n = 43

Problem 4 :

Shown below is a regular pentagon ABCDE

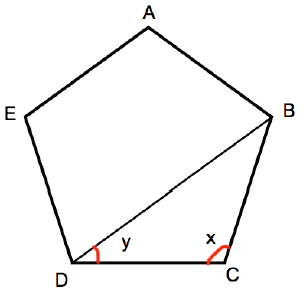
Solution :

Number of sides of given polygon = 5

Sum of interior angles = (n - 2) x 180

= (5 - 2) x 180

= 3 x 180

= 540

Measure of each angle = 540/5

x = 108

In triangle BDC,

DC = BC

∠BDC + ∠DCB + ∠CBD = 180

∠BDC = ∠CBD

y + x + y = 180

2y + x = 180

2y + 108 = 180

2y = 180 - 108

2y = 72

Dividing by 2 on both sides.

y = 72/2

y = 36

Problem 5 :

Shown below is a regular hexagon, with an exterior angle labeled y.

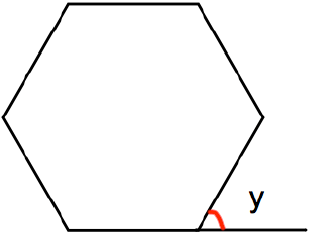
Work out the size of each exterior angle.

Solution :

Number of sides of the polygon above = 6

Sum of the angles of the polygon = (6 - 2) x 180

= 4(180)

= 720

Measure of each angle = 720/6

= 120

Sum of interior angle + y = 180

120 + y = 180

y = 180 - 120

y = 60

Problem 6 :

Shown is a regular hexagon and a regular octagon.

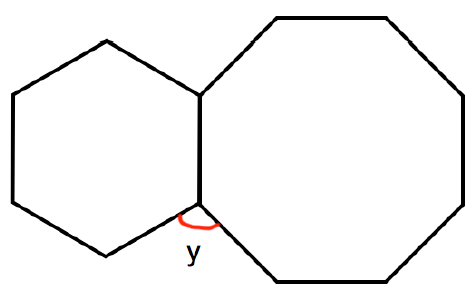
Solution :

Number of sides of hexagon = 6

Number of sides of octagon = 8

y = 360 - (120 + 135)

y = 360 - 255

y = 105

Problem 7 :

Shown below is a regular hexagon ABCDEF.

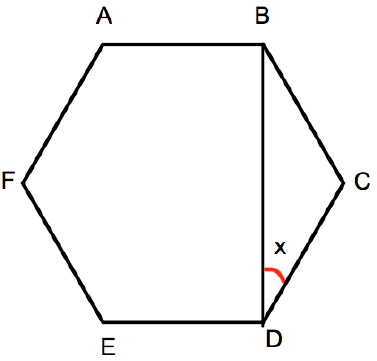
Calculate the angle x.

Solution :

Measure of each angle of hexagon = 120

Since it is regular polygon, CD = BC

∠CDB + ∠CBD + ∠BCD = 180

x + x + 120 = 180

2x + 120 = 180

Subtracting 120 on both sides.

2x = 180 - 120

2x = 60

Dividing by 2, we get

x = 60/2

x = 30