HOW TO FIND MULTIPLES OF A NUMBER BETWEEN THE TWO NUMBERS

Problem 1 :

Find the sum of integers from 1 to 500 which are multiple of 2 or 5.

Solution :

The sum of integers from 1 to 500 which are multiple of 2 or 5.

= Sum of numbers multiple of 2 + Sum of numbers multiple of 5 - Sum of numbers multiples of both 2 and 5.

Number of terms which are multiple of 2 between 1 to 500 :

2, 4, 6, 8, ..............500

a_n = a + (n – 1)d

500 = 2 + (n – 1)2

500 - 2 = (n - 1)2

n - 1 = 498/2

n = 249 + 1

n = 250

Number of terms which are multiple of 5 between 1 to 500 :

5, 10, 15, ..............500

a_n = a + (n – 1)d

500 = 5 + (n – 1)5

500 - 5 = (n - 1)5

(n - 1) = 495/5

n = 99 + 1

n = 100

Number of terms which are multiple of 2 and multiple of 5 :

10, 20, 30, …, 500

a_n = a + (n – 1)d

let a = 10, d = 10, a_n = 500

500 = 10 + (n – 1)10

500 = 10 + 10n – 10

500 = 10n

n = 500/10

n = 50

Problem 2 :

Find how many two – digit numbers are divisible by 6.

Solution :

To find two – digit numbers are divisible by 6.

The two – digit numbers are divisible by 6 is 12, 18, 24, …, 96.

a_n = a + (n – 1)d

let a = 12, d = 6, a_n = 96

96 = 12 + (n – 1)6

96 = 12 + 6n – 6

96 = 6 + 6n

Subtracting 6 on both sides.

96 – 6 = 6 – 6 + 6n

90 = 6n

Dividing 6 on each sides.

90/6 = 6/6n

15 = n

Therefore, two – digit numbers are divisible by 6 is 15.

Problem 3 :

Find the sum of all multiples of 7 lying between 500 and 900.

Solution :

To find sum of all multiples of 7 lying between 500 and 900.

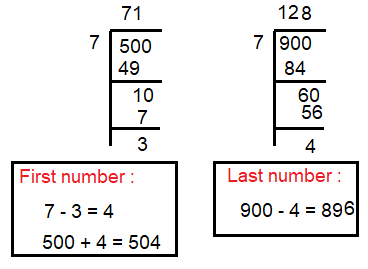
504, 511, 518, …, 896

First term a = 504

n^th term = 896

d = b – a

d = 511 – 504

d = 7 

a_n = a + (n – 1)d

let a = 504, d = 7, a_n = 896

896 = 504 + (n – 1)7

896 = 504 + 7n – 7

896 = 497 + 7n

399 = 7n

Dividing 7 on each sides.

399/7 = 7/7n

57 = n

Problem 4 :

Find the sum of first 40 positive integers divisible by 6.

Solution :

The first 40 positive integers divisible by 6 are 6, 12, 18, 24, ….

First term a = 6

d = 12 – 6 ==> 6

n = 40

S_n = (n/2) [2a + (n – 1)d]

S₄₀ = (40/2)[2(6) + (40 – 1)6]

= 20[12 + 39 × 6]

= 20[12 + 234]

= 4920