HOW TO FIND MISSING ANGLES OF RHOMBUS WITH DIAGONALS

What is rhombus ?

A rhombus is a quadrilateral in which all sides are equal is length.

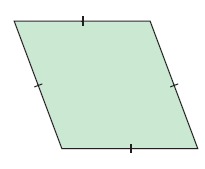
• Opposite angles are equal in size.
• Diagonals bisect each other at right angles.
• Diagonals bisect the angles at the vertex.

Find the all numbered angles in the following rhombus.

Problem 1 :

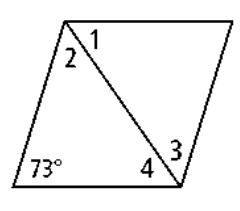
Solution :

Here ∠2 = ∠1, because the diagonal is the angle bisector.

∠2 = ∠4, because the equal sides will create equal angles.

∠4 = ∠3

73 + ∠2 + ∠4 = 180

73 + ∠2 + ∠2 = 180

73 + 2∠2 = 180

2∠2 = 180 - 73

2∠2 = 107

∠2 = 107/2 ==> 53.5

∠2 = 53.5

∠1 = 53.5

∠4 = 53.5

∠3 = 53.5

Problem 2 :

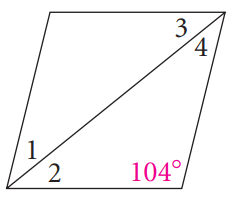
Solution :

∠2 = ∠4

In the triangle below,

∠2 + ∠4 + 104 = 180

∠4 + ∠4 = 180 - 104

2∠4 = 76

∠4 = 76/2

∠4 = 38

∠3 = 38 (angle bisector)

∠2 = 38 (Equal sides, will have same angles)

∠1 = 38 (Angle bisector)

Problem 3 :

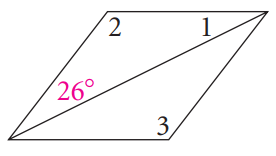
Solution :

In the triangle above, 

∠1 + ∠2 + 26 = 180

∠1 = 26

26 + ∠2 + 26  = 180

52 + ∠2 = 180

∠2 = 180 - 52

∠2 = 128

∠3 = 128 (Opposite angles)

Problem 4 :

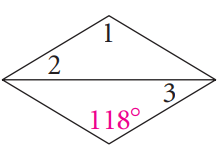
Solution :

∠1 = 118

∠1 + ∠2 + ∠2 = 180

118 + 2∠2 = 180

2∠2 = 180 - 118

2∠2 = 62

∠2 = 62/2

∠2 = 31

∠3 = 31

Problem 5 :

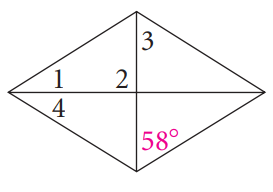
Solution :

From the figure given above, ∠3 = 58

∠2 = 90

∠1 + ∠2 + ∠3 = 180

∠1 + 90 + 58 = 180

∠1 + 148 = 180

∠1 = 180 - 148

∠1 = 32

∠4 = 32

Problem 6 :

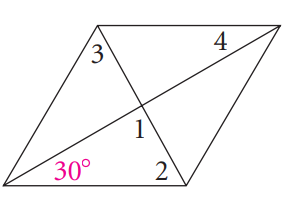
Solution :

∠2 = ∠3

Here ∠1 = 90

∠1 + 30 + ∠2 = 180

90 + 30 + ∠2 = 180

120 + ∠2 = 180

∠2 = 180 - 120

∠2 = 60

∠3 = 60

∠4 = 30

Problem 7 :

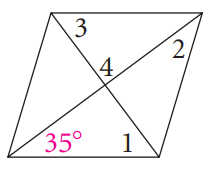
Solution :

∠4 = 90

∠2 = 35

∠3 + ∠4 + 35 = 180

∠3 + 90 + 35 = 180

∠3 + 125 = 180

∠3 = 180 - 125

∠3 = 55

∠1 = 55

Problem 8 :

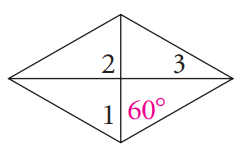
Solution :

∠2 = 90, ∠1 = 60

∠1 + ∠2 + ∠3 = 90

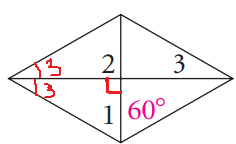60 + 90 + ∠3 = 180 150 + ∠3 = 180 ∠3 = 180 - 150 ∠3 = 30

Problem 9 :

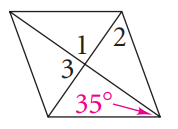
Solution :

∠1 = ∠3 = 90

In a triangle,

∠1 + ∠2 + 35 = 180

90 + ∠2 + 35 = 180

∠2 + 125 = 180

∠2 = 180 - 125

∠2 = 55

Problem 10 :

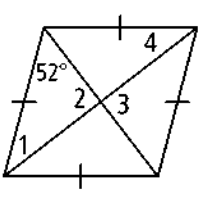
Solution :

∠1 = ∠4

∠1 + 52 + 52 + ∠4 = 180

∠1 + ∠1 + 104 = 180

2∠1 = 180 - 104

2∠1 = 76

∠1 = 76/2

∠1 = 38

∠2 = 90

∠3 = 90 (vertically opposite angles)