HOW TO FIND LOCAL MAX AND MIN FROM A GRAPH

Where local maximum will appear ?

A point is a local maximum point if the graph changes from increasing to decreasing at that point.

What is local maximum value ?

The local maximum value is the y-coordinate of the local maximum point.

Where local minimum will appear ?

A point is a local minimum point if the graph changes from decreasing to increasing at that point.

What is local minimum value ?

The local minimum value is the y-coordinate of the local minimum point

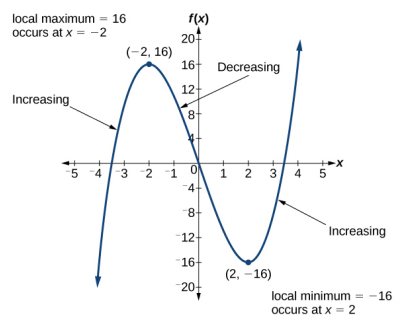
Problem 1 :

Use the graph of f(x) to determine:

a) interval(s) where the graph is increasing.

b) interval(s) where the graph is decreasing.

c) the coordinates of local maximum point, if any

d) the local maximum value

e) the coordinates of the local minimum point if any

f) the local minimum value

Solution :

By observing the graph, the graph is increasing then decreasing and increasing.

a) Increasing interval :

Increasing at (-∞, -2) and (2, ∞)

b) Decreasing interval :

Decreasing at (-2, 2)

c) Local maximum will appear when the function changes from increasing to decreasing.

Local maximum at x = -2

d) Local minimum will appear when the function changes from decreasing to increasing.

Local minimum at x = 2

e) Local maximum value is y = 16.

f) Local minimum value is y = -16.

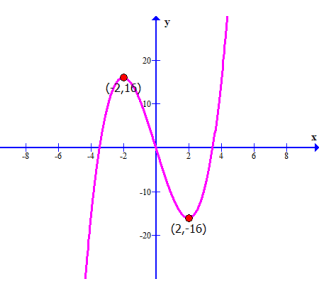
Problem 2 :

Find the

a) interval(s) where the graph is increasing.

b) interval(s) where the graph is decreasing.

c) the coordinates of local maximum point, if any

d) the local maximum value

e) the coordinates of the local minimum point if any

f) the local minimum value

Solution :

By observing the graph, the graph is increasing then decreasing and increasing.

a) Increasing interval :

Increasing at (-∞, -2) and (2, ∞)

b) Decreasing interval :

Decreasing at (-2, 2)

c) Local maximum will appear when the function changes from increasing to decreasing.

Local maximum at x = -2

d) Local minimum will appear when the function changes from decreasing to increasing.

Local minimum at x = 2

e) Local maximum value is y = 8.

f) Local minimum value is y = -8.

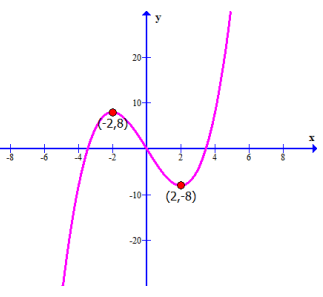
Problem 3 :

Find the following

a) interval(s) where the graph is increasing.

b) interval(s) where the graph is decreasing.

c) the coordinates of local maximum point, if any

d) the local maximum value

e) the coordinates of the local minimum point if any

f) the local minimum value

Solution :

By observing the graph, the graph is increasing then decreasing and increasing.

a) Increasing interval :

Increasing at (-∞, -3)

b) Decreasing interval :

Decreasing at (-3, ∞)

c) Local maximum will appear when the function changes from increasing to decreasing.

No local maximum

d) Local minimum will appear when the function changes from decreasing to increasing.

Local minimum at x = -3

e) No local maximum value

f) Local minimum value is y = 5.

Problem 4 :

Find the

a) interval(s) where the graph is increasing.

b) interval(s) where the graph is decreasing.

c) interval(s) where graph is constant

d) the coordinates of local maximum point if any

e) the local maximum value

f) the coordinates of the local minimum point if any

g) the local minimum value

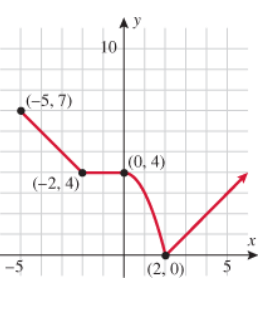
Solution :

a) Increasing at (2, ∞).

b) Decreasing at (-5, -2)

c) Constant at (-2, 0).

d) Local maximum at (-5, 7)

e) Local maximum value is at y = 7

f) Local minimum point is at (2, 0)

g) Local minimum value is at y = 0

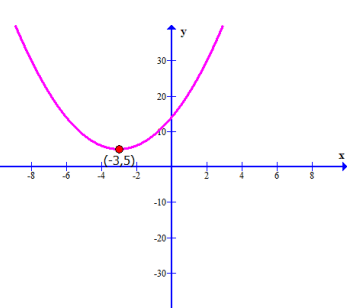
Problem 5 :

Find the

a) interval(s) where the graph is increasing.

b) interval(s) where the graph is decreasing.

c) the coordinates of local maximum point, if any

d) the local maximum value

e) the coordinates of the local minimum point if any

f) the local minimum value

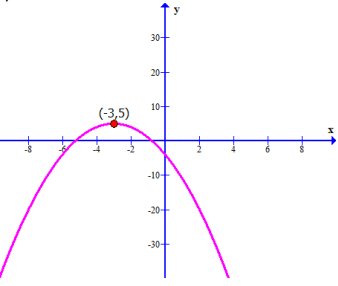
Solution :

a) Increasing is at (- ∞, -3)

b) Decreasing is at (-3, ∞) 

c) Local maximum point is (-3, 5)

d) Local maximum value is y = 5

e) Since there is no changes from decreasing to increasing, there is no local minimum.

f) No local minimum.

Problem 6 :

Find the

a) interval(s) where the graph is increasing.

b) interval(s) where the graph is decreasing.

c) the coordinates of local maximum point, if any

d) the local maximum value

e) the coordinates of the local minimum point if any

f) the local minimum value

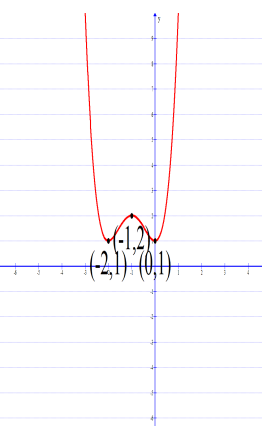
Solution :

a) Decreasing is at (-∞, -2) and (-1, 0)

b) Increasing is at (-2, -1) and (1, ∞)

c) local maximum point is (-1, 2)

d) the local maximum value is y = 2

e) The local minimum point is (-2, 1) and (0, 1)

f) the local minimum value is y = 1